2．能力目标：

(1)渗透数形结合、转化的数学思想，发展学生的符号感；　　

(2)在数学建模中培养学生的发散思维能力和创新思维能力.

根据上述教材结构与内容分析，依据新课标要求，考虑到学生已有的认知结构、心理特征 ，制定如下教学目标：

1．　 知识目标：

(1)理解平面直角坐标系及横、纵坐标、原点、坐标等概念；

(2)能画出平面直角坐标系；弄清象限内及坐标轴上点的坐标的符号特点；

(3)能在指定的坐标系中，由点的位置写出坐标，根据坐标描出相应的点；

(4)初步理解坐标平面内的点与“有序实数对”之间的一一对应关系.

本节内容在全章节的地位：本章是“函数及其图象”，主要内容是函数的基础知识，以及一次函数与反比例函数这两个基本函数的性质和简单应用.“平面直角坐标系”是在学习了“变量与函数”的基础上提出来的.平面直角坐标系概念的引入，标志着数学由常量数学向变量数学的迈进，这是学习数学知识的一个飞跃，有了平面直角坐标系，就可以把两个相依变化的量之间的变化规律,用图形非常形象地表示出来，，因此平面直角坐标系成了研究两个变量的有利工具和重要方法，也是数形结合思想的典型体现.所以说“平面直角坐系”是本章从函数过渡到图象的一个重要内容.

数学思想方法分析：作为一名数学老师,不仅要传授给学生数学知识,更重要的是传授给学生数学思想、数学意识，在课堂中教学注重数学思想方法的渗透，领悟数学知识发生与发展过程中的思想方法.因此本节课在教学中力图向学生展示观察、归纳、类比、联想等数学思想方法.

因为课堂教学是利用多媒体课件进行的，所以省略板书　

通过本节课的学习你有那些收获？

以提问的形式，学生归纳、总结，教师点评.

(设计意图：此时的学生反思课堂教学收获、自行归纳、总结，能达到升华知识的目的.)

(二)、填空

1、已知P点坐标为(2a+1，a-3)点P在x轴上，则a=　 ____________；点P在y轴上，则a= ____________；

2、若点P(x，y)在第四象限，|x|=5，|y|=4 则P点的坐标为____________.3、点A(3,1)到x轴的距离是____

4、点B(a, b)到y轴的距离是_____

5、到x轴的距离为2，到y轴的距离是3的点有___ ________个，它们是__________________.

(一)、判断：

1、对于坐标平面内的任一点，都有唯 一的一对有序实数与它对应.(　 　)

2、在直角坐标系内，原点的坐标是0.(　 　)　

3、点A(a ，-b　 )在第二象限，则点B(-a,b)在第四象限.　 (　 　)

4、若点P的坐标为(a，b)，且a·b=0，则点P一定在坐标原点.　 (　　　　 )

(一).平面直角坐标系有关概念　

1、我们已经知道，数轴上的点与实数是一一对应的.数轴上给定一个点就能找到它对应的一个实数，这个实数叫做这个点在数轴上的坐标，反过来，给定一个实数，就能在数轴上找到它所对应的一个点.大家想一想，一个实数我们可以用一条数轴上的一点来表示，那么，以上我们举的这些例子需要两个数来确定，你觉得应该用几条数轴来表示？

笛卡儿的方法是在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴，这就建立了平面直角坐标系.其中水平的数轴叫X轴(或横轴)取向右为正方向，铅直的数轴叫Y轴(或纵轴)，取向上为正方向，两条数轴的交点O叫做坐标原点.

(设计意图：由数轴上的点与实数的关系引入平面内的点的表示方法.通过旧知识引入新知识，承上启下.)

练习1：你能参照定义画一个平面直角坐标系吗？

(设计意图：让学生通过画平面直角坐标系，来进一步理解、掌握概念.充分体现教师为主导，学生为主体的教学理念.同时激励学生继续深入探究.)

教师启发学生联想已经学过的统计图知识，发现它们实际上已经具备了直角坐标系的所有要素.

(设计意图：加强与学生已有知识的联系，让学生产生亲近感，认同新概念并纳入自己的知识范围.)

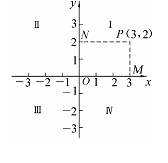
2、任取平面内一点，我们都可以用一对有序实数来描述它的位置.如点P，从P点分别向x轴与y轴作垂线，垂足分别为M、N，点M、N在x轴与y轴上所的对应的数，就是点P的横坐标与纵坐标，由此得出的有序实数对就是点P的坐标P(3，2).在直角坐标系中，两条坐标轴把平面分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域，分别称为第一、二、三、四象限.坐标轴上的点不属于任何一个象限.

练习2：写出图中P，B，C，D，E，F各点的坐标.

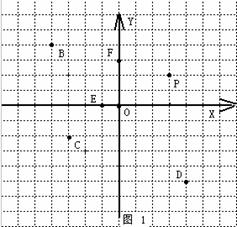
(设计意图：巩固所学知识，同时激励学生继续深入探究.)

2、解决相关问题

例1　分别在平面内描出坐标是(2，3)、(-2，3)(3，-2)的点Q、S、R，Q(2，3)与P(3，2)是同一点吗？S(-2，3)与R(3，-2)是同一点吗？

教师鼓励学生充分发表意见，由此体会和理解“有序实数对”的意义.

例2　写出平面直角坐标系中的A、B、C、E、F各点的坐标.

观察你所求出的这些点的坐标,回答下列问题:

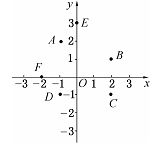(1)象限内的点有什么特征？

(2)坐标轴上的点有什么特征？

让学生自行探索、交流，师生总结归纳：

(1)第一象限的点的坐标为(+、+) 　　　 　第二象限的点的坐标为(－、+) 　　　　 第三象限的点的坐标为(－、－) 　　　　 第四象限的点的坐标为(+、－)

(2)x轴上点的纵坐标等于0；y轴上点的横坐标等于0；

(设计意图：通过学生的自主探究，培养学生的科学探究能力.)

练习3：

(1)点A(2，-3)在第 ____ 象限.

(2)点C(a-1，-b+3)在X轴上，则b=　 ____ .

若点D(-3a-1，-2b+3)在Y轴上，则a= ____ .

(3)点P(4a-8，1-2 a)是第三象限的点，且a是整数，a= ____ .

(设计意图：加强学生对象限内点的特征、坐标轴上点的特征的理解和记忆，提高课堂教学效益.)

归纳：通过上面例题的讲解，大家知道对于坐标平面内的任意一点，有唯一的一对有序实数与它对应，对于任意一对有序实数，坐标平面内有唯一的一点与它对应.回忆数轴上的点与实数的一一对应关系，我们可以说坐标平面内的点与有序实数对是一一对应的.

课件出示一排队伍，问：要表示某个队员的位置，应该怎么说？需要用多少个数来表示？这与数轴上的点和实数有什么样的联系？

再出示几排队伍，问：要表示某个队员的位置，应该怎么说？需要用多少个数来表示？

学生回答，教师总结：一排队伍要表示某个队员的位置用一个数来表示，这与一条数轴上要表示某个点的位置是相似的.几排队伍里要表示某个队员的位置需要用两个数来表示，我们把这两个数称一对有序实数.

(设计意图：从学生熟识的生活实际出发，创设情境，激发学生学习兴趣，让学生具体感知从一维到二维的发展.)

再举出几个生活中需要两个数来确定位置的例子，如：电影院的座位，教室的座位，门牌号，象棋、围棋的棋谱等.

(设计意图：举一些生活中的实例，丰富学生的感性认识.)

上面的例子，我们都可以归结为如何用两个实数来确定平面上的点的位置问题.那么数学上是怎样解决这个问题呢？早在1637年以前，法国数学家笛卡儿受到了经、纬线的启发，建立了“笛卡儿直角坐标系”,这就是今天我们要研究平面直角坐标系.

(设计意图：通过介绍笛卡儿创立直角坐标系的背景知识，激励学生敢于探索，勇攀科学高峰.)

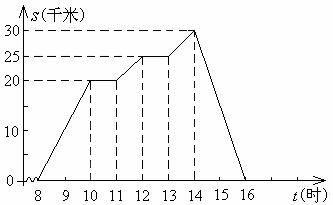
4.周末，小李8时骑自行车从家里出发，到野外郊游，16时回到家里．他离开家后的距离S(千米)与时间t(时)的关系可以用图中的曲线表示．根据这个图象回答下列问题：

(1)小李到达离家最远的地方是什么时间？

(2)小李何时第一次休息？

(3)10时到13时，小骑了多少千米？

(4)返回时，小李的平均车速是多少？