
4、回顾反思,整体评价
今天我们掌握了相似多边形的特征,如何利用这个特征求线段的长度?又如何判别两个多边形相似呢?
(让学生总结,通过问题的回答,引导学生自主总结,把分散的知识系统化、结构化,形成知识网络,完善学生的认知结构,加深对所学知识的理解.)
3、知识迁移,拓展思维
基础练习:P70 3、4、5.
思维拓展:
(1)讨论:①两个三角形一定是相似形吗?两个等腰三角形呢?两个等边三角形呢?
②所有的矩形都相似吗?所有的正方形呢?
(2)思考:工人师傅按照比例尺为1:2的图纸制作三角形零件.如图所示,该零件的横截面为△ABC,画在图纸上是△DEF,CH、FG分别是它们的高。

①找出图中的相似三角形,并简述理由.
②CH与FG的比是多少?
③你发现了什么?与同伴交流。
(通过知识的综合应用,拓宽学生的视野,提高他们灵活运用知识的能力,培养学生的发散思维。)
2、探索研究,揭示特征
相似图形的特征
(1)提出猜想:
上节课我们研究了P67两张相似地图中的对应线段AB与A′B′、BC与B′C′、AC与A′C′的比相等,即
请你由此猜想两张相似地图中的对应线段有什么关系?
――显然,两张相似地图中的对应线段都是成比例的.
这个结论对一般的相似多边形是否成立呢?我们不妨通过下面测量与计算来说明.
(2)进行验证:
仔细观察下面两幅图形,量一量、算一算它们的对应边之间是否有以上的关系?对应角之间又有什么关系呢?

通过测量与计算,我们可得:
图(一)中:
且 ∠A=∠A′ ∠B=∠B′∠C=∠C′∠D=∠D′
图(二)中:
且 ∠A=∠A′ ∠B=∠B′∠C=∠C′∠D=∠D′∠E=∠E′
即:相似四边形、相似五边形的对应边各成比例,对应角各相等.
思考与讨论
①由此可知两个相似多边形的特征是什么?
(对应边成比例,对应角相等.)
②由相似多边形的特征可否得到识别两个多边形是否相似的方法?举例说明.
(如果两个多边形的对应边成比例且对应角相等,那么这两个多边形相似.)
实践运用
议一议 观察下面两组图形,各组图形是否相似?为什么?与同伴交流.
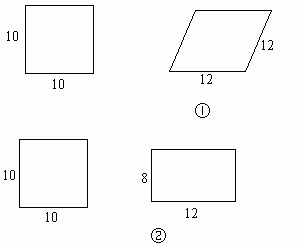
(通过学生的交流,培养他们的合作精神和欣赏他人的意识.)
思考: 如果两个多边形不相似,那么它们的对应角有可能都相等吗?对应边有可能都成比例吗?
做一做 一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木质边框宽7.5m.边框的内外边缘所成的矩形相似吗?为什么?

(动手操作,体验数学活动的探索性和创新性.)
算一算
(1)测量旗杆的问题:

如图,三角形OCD与三角形OAB相似,由相似多边形的特征可得: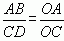
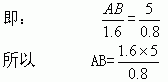
即: AB=10(米)
答:旗杆的高度AB为10米.
(2)P69例1.在下图所示的相似四边形中求未知边x、y的长度和角度a的大小.
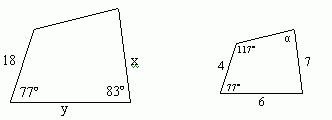
分析:由相似多边形的特征可得: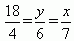 ,则可分别求出x、y.再由相似多边形的对应角相等及四边形的内角和为360º,即可求出角度
,则可分别求出x、y.再由相似多边形的对应角相等及四边形的内角和为360º,即可求出角度 的大小.
的大小.
(让学生板书,并参阅P69)
解:(略)
(通过知识的直接运用及训练巩固,使知识融会贯通。)
1、创设情境,设疑激趣
(多媒体演示)
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许很想知道,操场上的旗杆到底有多高呢?

通常一种简便的方法是:如下图所示,站在操场上,请你的同学量出你在太阳下的影子长度OC、旗杆的影子长度OA,再量出你的身高CD,根据三角形OCD与三角形OAB相似,就可以计算出旗杆的高度AB了.
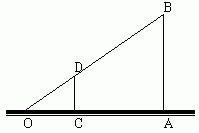
如果测得OC= 0.8米,OA=5米,CD=1.6米,如何求AB的高呢?
下面我们一起来研究、解决这个问题.
(通过多媒体的直观演示,设置问题情境,营造良好的课堂气氛,激发学生的学习兴趣。)
多媒体电教及教学软件
多媒体教学--创设情境,以境激趣
探索教学法--调动学生主动参与探索知识、运用知识过程
教学重点:探索并掌握相似图形的特征.
教学难点:探索与研究问题的思维方式.
3.培养学生“观察-猜想-验证-实践”的研究问题的思维方式.
2.通过实践,掌握利用相似图形的特征计算边的长度或角的度数.
1.经历自主探索相似图形的特征的过程,理解相似多边形对应角相等、对应边成比例以及面积比的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com