
4. 判定一个直角三角形,除了可根据定义去证明它有一个直角外,还可以采用勾股定理的逆定理,即去证明三角形两条较短边的平方和等于较长边的平方,这是代数方法在几何中的应用.
 e线聚焦
e线聚焦
[例]如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
分析:根据题目所给数据特征,联想勾股数,连接AC,可实现四边形向三角形转化,并运用勾股定理的逆定理可判定△ACD是直角三角形.
 解:连接AC,在Rt△ABC中,
解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25, ∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
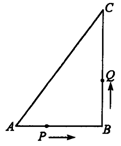
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD=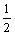 AB·BC+
AB·BC+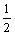 AC·CD=
AC·CD=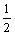 ×3×4+
×3×4+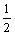 ×5×12=6+30=36.
×5×12=6+30=36.
 双基淘宝
双基淘宝
u 仔细读题,一定要选择最佳答案哟!
3. 应用勾股定理的逆定理时,先计算较小两边的平方和再把它和最大边的平方比较.
2. 满足a2 +b2=c2的三个正整数,称为勾股数.勾股数扩大相同倍数后,仍为勾股数.常用的勾股数有3、4、5、;6、8、10;5、12、13等.
1.勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
18.2 勾股定理的逆定理(1)
 知识领航
知识领航
11.能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数,观察下列表格所给出的三个数a,b,c,a<b<c.
(1)试找出它们的共同点,并证明你的结论.
(2)写出当a=17时,b,c的值.
10.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
◆拓展创新
|
3,4,5 |
32+42=52 |
|
5,12,13 |
52+122=132 |
|
7,24,25 |
72+242=252 |
|
9,40,41 |
92+402=412 |
|
… |
… |
|
17,b,c |
172+b2=c2 |
9.写出下列命题的逆命题,并判断真假.
(1)如果a=0,那么ab=0;
(2)如果x=4,那么x2=16;
(3)面积相等的三角形是全等三角形;
(4)如果三角形有一个内角是钝角,则其余两个角是锐角;
(5)在一个三角形中,等角对等边.
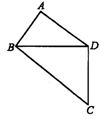
8.如图所示,四边形ABCD中,BA⊥DA,AB=2,AD=2 ,CD=3,BC=5,求∠ADC的度数.
,CD=3,BC=5,求∠ADC的度数.
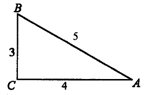
7.A,B,C三地的位置及两两之间的距离如图所示,则点C在点B的方位是_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com