5．若三角形的两边长为4和5，要使其成为直角三角形，则第三边的长为　　　　 .

4．将勾股数3，4，5扩大2倍，3倍，4倍，…，可以得到勾股数6，8，10；9，12，15；12，16，20；…，则我们把3，4，5这样的勾股数称为基本勾股数，请你也写出三组基本勾股数　　　　　　 ,　　　　　　 ,　　　　　　　 .

3. 有六根细木棒，它们的长度分别为2，4，6，8，10，12(单位：cm)，从中取出三根首尾顺次连接搭成一个直角三角形，则这根木棒的长度分别为(　　 )

　 　A．2，4，8　　　 　　B.4,8,10　　　　　　 C.6,8,10　　　　　 D.8,10,12

2．在下列说法中是错误的(　 )

　 　A．在△ABC中，∠C＝∠A一∠B，则△ABC为直角三角形.

　　 B．在△ABC中，若∠A：∠B：∠C＝5：2：3，则△ABC为直角三角形.

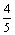　　 C．在△ABC中，若a＝c，b＝c，则△ABC为直角三角形.

　　 D．在△ABC中，若a：b：c＝2：2：4，则△ABC为直角三角形.

1.　 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是( 　　)

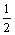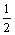A.7,24,25　 　　　B.3,4,5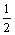　 　　　C.3,4,5　 　　　　D.4,7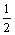,8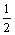

2．体会从“形”到“数”和从“数”到“形”的转化，培养转化、推理的能力.

　e线聚焦

　　 [例]如图，南北向MN为我国领域，即MN以西为我国领海，以东为公海.上午9时50分，我反走私A艇发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里，A、B两艇的距离是5海里；反走私艇测得离C艇的距离是12海里.若走私艇C的速度不变，最早会在什么时间进入我国领海？

分析：为减小思考问题的“跨度”，可将原问题分解成下述“子问题”：(1)△ABC是什么类型的三角形？(2)走私艇C进入我领海的最近距离是多少？(3)走私艇C最早会在什么时间进入？这样问题就可迎刃而解.

解：设MN交AC于E，则∠BEC=90⁰.

又AB²+BC²=5²+12²=169=13²=AC²，

∴△ABC是直角三角形，∠ABC=90⁰.

又∵MN⊥CE，∴走私艇C进入我领海的最近距离是CE，

则CE²+BE²=144，(13-CE)²+BE²=25，得26CE=288，

∴CE=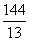.　　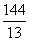 ÷≈0.85(小时)，　 0.85×60=51(分).

9时50分+51分=10时41分.

答：走私艇最早在10时41分进入我国领海.

双基淘宝

u　　　　 仔细读题，一定要选择最佳答案哟！

1．应用勾股定理及其逆定理解决简单的实际问题，建立数学模型．

18.2　勾股定理的逆定理(2)

　知识领航

10．如图，在△ABC中，∠ACB=90º，AC=BC，P是△ABC内的一点，且PB=1，PC=2，PA=3，求∠BPC的度数．

9．如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上的C处有一筐水果，一只猴子从D处上爬到树顶A处，利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处滑到地面B，再由B跑到C，已知两猴子所经路程都是15m，求树高AB.

拓广创新

u　　　　 试一试，你一定能成功哟！