活动1　 (1)总结直角三角形有哪些性质． (2)一个三角形，满足什么条件是直角三角形?

设计意图：通过对前面所学知识的归纳总结，联想到用三边的关系是否可以判断一个三角形为直角三角形，提高学生发现反思问题的能力．

师生行为　　 学生分组讨论，交流总结；教师引导学生回忆．

本活动，教师应重点关注学生： ①能否积极主动地回忆，总结前面学过的旧知识； ②能否“温故知新”．

　　 生：直角三角形有如下性质：(1)有一个角是直角；(2)两个锐角互余，(3)两直角边的平方和等于斜边的平方： (4)在含30°角的直角三角形中，30°的角所对的直角边是斜边的一半．

　　 师：那么，一个三角形满足什么条件，才能是直角三角形呢?

　　 生：有一个内角是90°，那么这个三角形就为直角三角形．

　　 生：如果一个三角形，有两个角的和是90°，那么这个三角形也是直角三角形．

　　 师：前面我们刚学习了勾股定理，知道一个直角三角形的两直角边a，b斜边c具有一定的数量关系即a²+b²＝c²，我们是否可以不用角，而用三角形三边的关系来判定它是否为直角三角形呢?我们来看一下古埃及人如何做?

教学重点 探究勾股定理的逆定理，理解互逆命题，原命题、逆命题的有关概念及关系．

教学难点 归纳、猜想出命题2的结论．

教具准备 　多媒体课件．

教学过程

5.3或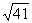　 6.120cm² 7.由BD²+DC²=12²+16²=20²=BC²得CD⊥AB又AC=AB=BD+AD=12+AD，在Rt△ADC中，AC²=AD²+DC²，即(12+AD)²=AD²+16²，解得AD=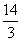，故 △ABC的周长为2AB+BC=cm　　 8.由勾股定理的逆定理可判定△ABC是直角三角形，由面积关系可求出公路的最短距离BD=km， ∴最低造价为120000元　　 9.设AD=x米，则AB为(10+x)米，AC为(15-x)米，BC为5米，∴(x+10)²+5²=(15-x)²，解得x=2，∴10+x=12(米)　　　 10．如图，将△APC绕点C旋转，使CA与CB重合，即△APC≌△BEC,∴△PCE为等腰Rt△，∴∠CPE=45°，PE²=PC²+CE²=8. 又∵PB²=1，BE²=9，∴PE²+ PB²= BE²,则∠BPE=90°，∴∠BPC=135°.

1.B 　　2.D 　3.C 　4.5，12，13; 8，15，17; 11，60，61(此题答案不唯一)

18.2　勾股定理的逆定理(2)

10．如图，在△ABC中，∠ACB=90º，AC=BC，P是△ABC内的一点，且PB=1，PC=2，PA=3，求∠BPC的度数．

9．如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上的C处有一筐水果，一只猴子从D处上爬到树顶A处，利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处滑到地面B，再由B跑到C，已知两猴子所经路程都是15m，求树高AB.

拓广创新

u　　　　 试一试，你一定能成功哟！

8．如图，三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km，求修这条公路的最低造价是多少？

7．如图，已知等腰△ABC的底边BC=20cm，D是腰AB上一点，且CD=16cm，BD=12cm，求△ABC的周长.