2、使学生掌握预备定理，并了解它的承上启下的地位和作用。

1、使学生理解并掌握相似三角形的概念，理解相似比的概念。

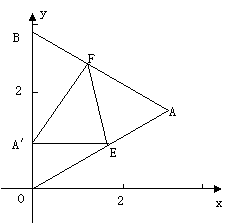
25．如图，△OAB是边长为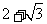的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在边OB上，记为A′，折痕为EF.

⑴　当A′E∥x轴时，求点A′和E的坐标；

⑵　当A′E∥x轴，且抛物线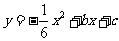经过点A′和E时，求该抛物线与x轴的交点的坐标；

⑶　当点A′在OB上运动但不与点O、B重合时，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明现由.

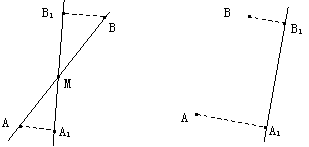
24．某供电部门准备在输电主干线l上连接一个分支线路，分支点为M，同时向新落成的A、B两个居民小区送电.已知居民小区A、B分别到主干线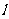的距离AA₁＝2千米，BB₁＝1千米，且A₁B₁＝4千米.

⑴　如果居民小区A、B在主干线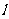的两旁，如图⑴所示，那么分支点M在什么地方时总线路最短？最短线路的长度是多少千米？

⑵　如果居民小区A、B在主干线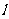的同旁，如图⑵　示，那么分支点M在什么地方时总线路最短？此时分支点M与A₁的距离是多少千米？

23．某汽车停车场预计“十·一”国庆节这天将停放大小汽车1200辆次，该停车场的收费标准为：大车每辆次10元，小车每辆次5元.根据预计，解答下面的问题：

⑴　写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式，并指出自变量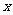的取值范围；

⑵　如果国庆节这天停放的小车辆次占停车总辆次的65%-85%，请你估计国庆节这天该停车场收费金额的范围.

22．将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上.

⑴　随机地抽取一张，求P(奇数)；

⑵　随机地抽取一张作为十位上的数字(不放回)，再抽取一张作为个位上的数字，能组成哪些两位数？恰好是“32”的概率为多少？

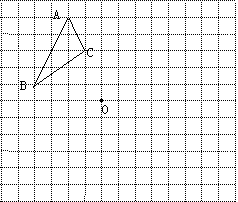
1．在下面的网格图中按要求画出图形，并回答问题：

⑴　先画出△ABC向下平移5格后的△A₁B₁C₁，再画出△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△A₂B₂C₂；

⑵　在与同学交流时，你打算如何描述⑴中所画的△A₂B₂C₂ 的位置？

4、老师给出一个函数，甲、乙、丙各正确地指出了这个函数的的一个性质：

甲：函数的图象经过第一象限；　　　　 乙：函数的图象经过第二象限

丙：在每个象限内，y随着x的增大而减小.

请你根据他们的叙述构造满足上述性质的一个函数：　　　　　　　　　　 .

3、观察下面的点阵图和相应的等式，探究其中的规律：

⑴在④和⑤后面的横线上分别写出相应的等式；

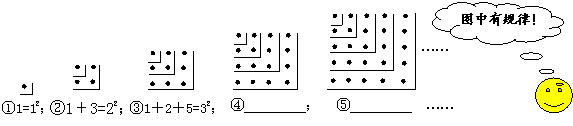
⑵通过猜想写出与第n个点阵相对应的等式.　　　　　　　　　　　　　　 。

2、如图，如果横行上的两个数字之和相等，竖列上的两个数字之和相等，那么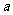、、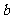、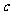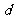依次可为　　　　　　　　 .(只需填写一组你认为合适的数字即可).