2、探索研究，形成新知

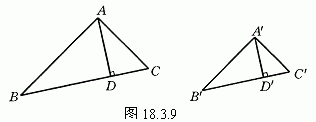
△ABD和△A′B′D′都是直角三角形，而∠B＝∠B′，因为有两个角对应相等，所以这两个三角形相似．那么

由此可以得出结论： 相似三角形对应高的比等于相似比．

　　(通过研究讨论，让学生借助已有的知识对新问题进行研究，培养学生的思考探索能力，同时让他们自己得出结论，感受成功的喜悦。)

思 考

　　 图18.3.11中，△ABC和△A′B′C′相似，AD、A′D′分别为对应边上

的中线，BE、B′E′分别为对应角的角平分线，那么它们之间有什么关系呢？

　　 可以得到的结论是_________________________________________．

　　 想一想： 两个相似三角形的周长比是什么？

　　 可以得到的结论是_________________________________________．

　　 (让学生用类似于“相似三角形对应高的比等于相似比”的方法进行研究，培养学生的推理能力。)

1、创设情境，设疑激趣

两个三角形相似，除了对应边成比例、对应角相等之外，还可以得到许多有用的结果．例如，在图18.3.9中，△ABC和△A′B′C′是两个相似三角形，相似比为k，其中AD、A′D′分别为BC、B′C′边上的高，那么AD、 A′D′之间有什么关系？

教学重点：相似三角形的各条性质的掌握

教学难点：相似三角形性质中面积比的结论的得出。

2.　　　 运用相似三角形性质解决简单的问题。

1.　　　 利用前面几节的相关结论经过简单的推导得出相似三角形的各条性质；

(二)在相似多边形中，最为简单的就是相似三角形(similar triangle)．

什么是相似三角形呢？前面我们学过形状相同的图形说成是相似的图形，而相似三角形的本质特征就是“具有相同的形状”，它们的大小不一定相等。

(为加深学生对相似三角形的概念的本质的认识，教学时预先准备几对相似三角形，让学生观察或测量对应元素的关系。)

定义：对应边相等、对应角成比例的三角形是相似三角形。

(注意：定义中要求有两个条件，缺一不可)

(1)表示：相似用符号“∽”来表示，读作“相似于”．如图18.3.1所示的两个三角形中，

∠A＝∠A′， ∠B＝∠B′，∠C＝∠C′，

即△ABC与△A′B′C′相似，记作

△　　 ABC∽△A′B′C′，

读作“△ABC相似于△A′B′C′”．

　　 (强调：用“∽”表示两个三角形相似时，表示对应顶点的字母一定要写在对应的位置上，这样可准确地找出相似三角形的对应角和对应边)

(2)相似比：如果记＝k，那么这个比值k就表示这两个相似三角形的相似比．

注：两个相似三角形的相似比具有顺序性。即：若　 △ABC 与 △DEF 的相似比 k ，则△DEF 与△ABC 的相似比为1：k

2.巩固应用，拓展研究

思考：△ABC ∽△DEF，AB=7，DE=21，

(1)　　 求△ABC 与 △DEF 的相似比是多少？

(2)　　 若AC=6，求DE的长；

(3)　　 若AC=6，EF=24，求△ABC 与 △DEF 的周长分别是多少？△ABC 与 △DEF 的周长比是多少？它与相似比有什么关系？

(4)　　 △DEF 的周长与△ABC的周长为40，分别求△ABC 与 △DEF 的周长各是多少？

通过此题的练习，使学生掌握以下几点：

练习(1)、(2)对相似三角形的概念、表示及特征的分析，理解相似比；

练习(3)的操作后，使学生明白相似三角形的周长比等于其相似比；此题的方法不唯一，可以先分别算出△ABC 的各边长与 △DEF 的各边长，然后再分别求出其周长；也可以直接考虑周长：由＝k可知，A B=k• A′B′， B C= k•B′C′，C A=k• C′A′，所以

练习(4)是上面几题的应用，可通过周长比等于相似比及周长差为40两个条件组成一个二元一次方程组的思想。

(通过几个问题的设置，使学生掌握相关的知识概念，加深对新知识理解与应用。)

3.练习巩固，促进迁移

做一做　 如图18.3.2，△ABC中，D为边AB上任一点，作DE∥BC，交边AC于E，用刻度尺和量角器量一量，判断△ADE与△ABC是否相似.

我们知道，根据两直线平行同位角相等，则

∠ADE＝∠ABC， ∠AED＝∠ACB，而∠A＝∠A．

　 通过度量，还可以发现它们的对应边成比例，所以△ADE∽△ABC.

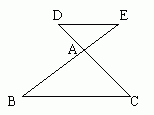
类似的，在图中当 ED∥BC时，△ADE ∽ △ABC　 。因此我们得到下面的定理：

预备定理：平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似。

如果取点D为边AB的中点，那么上题中△ADE和△ABC的相似比就为k

＝.

当k＝1时，这两个三角形不仅形状相同，而且大小也相同，这样的三角形

我们就称为全等三角形(congruent triangles)．全等三角形是相似三角形的特例.

4.应用巩固，课内深化

(1)判断下面两个三角形是否相似，简单说明理由：

(2)如果一个三角形的三边长分别是5、12和13，与其相似的三角形的最长边长是39，那么较大三角形的周长是多少？较小三角形与较大三角形周长的比是多少？

(3)已知一个三角形的三边之比为3：5：7，和它相似的另一个三角形的最大边长为14cm，求它的最小边长为多少？

(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P36第10题)

(4)一油桐高1m，桶内有油，一根木棒长为1.2m从桶盖的小口斜插入桶中，一端到桶底，另一端到小口，量得浸油部分长0.45m，求桶内油的高度为多少？(假设插入的木棒对油面高度无影响)

(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P37第14题)

5.回顾联系，形成结构

想一想：本节课学了哪些知识？

(通过问题的回答，引导学生自主总结，把分散的知识系统化、结构化，形成知识网络，完善学生的认知结构，加深对所学知识的理解．)

6.课外作业与拓展

参见励耘精品系列丛书《课时导航》华师大版八年级(下)P36－P37

(一)相似图形的特征是什么？

(学生回顾相关知识，为相似三角形的研究做好准备。)

1.复习回顾，概括概念

教学重点：相似三角形的概念及预备定理。

教学难点：由相似三角形写对应边的比例式。

3、通过预备定理的条件所构成的图形的三种情况，教学生对一致性问题的思想方法。