
5.学习小结
 (1)内容总结
(1)内容总结
一次函数、正比例函数 图象的特征
图象的画法
(2)方法归纳
画一次函数图象时,只要在图象上找到两点的坐标,在坐标系中描出这两点,再经过这两点画直线即可.
4.达标反馈
(多媒体演示)
(1)正比例函数y=kx(k≠0)的图象是经过( 0,0 )和点 (1,k)的一条直线.
(2)一次函数y=kx+b(k≠0)的图象是经过点 (0,b)且与直线y=kx 平行 的直线.
(3)画出下列各组一次函数的图象,并说出它们有什么关系.
①y=-2x-1与y=-2x+6. ②y=x+3与y=-3x+3.
答案:①平行,位置不同 ②相交,交点在y轴上.
3.合作探究
(1)整体感知
上节课我们主要学习了一次函数、正比例函数的概念,这节课我们将着重探讨一次函数与正比例函数图象的主要特征及其图象的画法.
(2)四边互动
互动1
师:利用多媒体演示幻灯片“做一做”内容.
做一做:在同一个平面直角坐标系中画出下列函数的图象.
(1)y=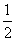 x; (2)y=
x; (2)y=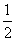 x+2;
(3)y=3x; (4)y=3x+2.
x+2;
(3)y=3x; (4)y=3x+2.
通过画图,你发现一次函数、正比例函数的图象的形状分别是什么?
生:动手操作,在几何练习簿上建立坐标系,用描点法画出上述函数的图象,在小组之间展开交流讨论,推选代表表达小组归纳的结论.
明确 师生共同概括:根据以上实践、观察与讨论,我们发现一次函数y=kx+b(k≠0)的图象是一条直线.通常也称为直线y=kx+b.特别地,正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线.值得注意的是:一次函数的图象不可能与坐标轴平行.
互动2
师:利用多媒体演示幻灯片.
认真观察上述画出的四个函数图象的特点,比较下列各对函数图象的相同点和不同点:
(1)y=3x与y=3x+2; (2)y=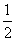 x与y=
x与y=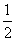 x+2; (3)y=3x+2与y=
x+2; (3)y=3x+2与y=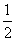 x+2.
x+2.
由此你发现什么规律?
生:在小组之间展开交流与讨论,各组推选代表发言.
师:利用多媒体演示“一次函数图象的平移”课件(华东师范大学出版社教学光盘),验证同学们的猜想.
明确 在第(1)组和第(2)组中的两个函数图象平行,但位置不同,可以通过相互平移得到;在第(3)组的两个函数图象相交,且交点在y轴上.
概括归纳可知:对于一次函数y=kx+b和y=k1x+b1,
(1)当k=k1,b≠b1时,两条直线平行,可以通过平移其中一条直线得到另一条直线;
(2)当k≠k1,b=b1时,两条直线相交,且交点在y轴上,是(0,b).
互动3
师:利用多媒体演示幻灯片.
(1)直线y=2x-3可以由直线y=2x经过 向下平移3个单位 而得到;直线y=-3x+2可以由直线y=-3x经过 向上平移2个单位 而得到;直线y=x+2可以由直线y=x-3经过 向下平移5个单位 而得到.
(2)直线y=2x+5与直线y=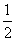 x+5都经过y轴上的同一点(
0, 5 ).
x+5都经过y轴上的同一点(
0, 5 ).
(3)将直线y=-2x-1向上平移3个单位,得到的直线是 y=-2x+2.
生:动手尝试,在4人小组中交流结果,然后举手回答解题思路和结果.
明确 教师利用多媒体逐个点击答案,验证同学们操作结果的正确性.
互动4
师:利用多媒体演示幻灯片.
[例1]在同一平面直角坐标系中画下列函数的图象.
(1)y=2x与y=2x+3; (2)y=2x+1与y=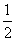 x+1.
x+1.
师:(点拨)画一次函数和正比例函数的图象,我们还需要用描点法吗?只要在图象上分别找到几点就可以确定其图象的位置?
生:动手操作,并交流操作的结果.
明确 教师利用多媒体演示操作的过程和结果.
归纳:由于一次函数是直线,因此在画其图象时,只要在图象上找到两点,便可以画出它的图象,通常所取的两点是图象与坐标轴的两个交点;特别地,由于正比例函数的图象是经过原点的一条直线,因此画其图象时,只要找到异于原点(0,0)的一点的坐标即可,通常所取的点是(1,k).
互动5
师:请同学们完成课本第42页的练习.
生:动手操作,在小组之间展开交流和互评.
明确 教师利用多媒体演示练习的答案,并口述解题过程和应注意的事项.
把练习的第1题与例1作出的图象比较可知:
对于直线y=kx+b(k≠0),当k>0时,图象可形象说成“撇”;当k<0时,图象可想像地说成“捺”;当b>0时,直线与y轴的交点位于x轴的上方;当b<0时,直线与y轴的交点位于x轴的下方;当b=0时,直线经过坐标系原点.
2.课前热身
回顾:在未知函数图象的具体形状的情况下,怎样画出一个给定的函数的图象?一般可以分为哪几个步骤?
答案:用“描点法”画函数图象,可以分成“列表、描点、连线”三个步骤.
1.情境导入
如图17-3-2所示,已知A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,你知道A、B两人所跑的路程s(米)与时间t(秒)之间属于哪种函数关系吗?

3.了解直线y=kx+b(k≠0)中k、b的几何意义.
2.会画一次函数、正比例函数的图象.
1.经历探究画一次函数图象的过程,了解一次函数、正比例函数的图象特征.毛
(四)板书设计:毛
┌────────────────┬────┐
│课题 │ │
│一次函数、正比例函数的意义 │ │
│一次函数、正比例函数的表达形式 │ 投影幕 │
├────────────────┤ │
│学生板演内容 │ │
└────────────────┴────┘
(三)拓展延伸
1.链接生活
为了加强公民节约用水意识,某市制定了如下收费标准:每户每月用水不超过10吨时,每吨水收费1.2元;超过10吨时,超过部分每吨按1.8元收费.该市某住户3月份用水超过10吨,那么该住户3月份应缴水费多少元?
答案:设该用户3月份用水x吨
y=10×1.2+(x-10)×1.8
=1.8x-3(x≥10)
2.实践探索
(1)实践活动
请收集有关一次函数在社会生活中应用的两个实例,列出函数关系式,然后解答问题.
(2)巩固练习
课本第47页习题17.3第1-3题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com