3．总结探索的结论：你发现两个相似三角形的对应边和对应角各有什么关系？用一句话概括。

2．学生探索：请根据这两个相似三角形为例进行探索，并在小组内交流和讨论。

先找出他们的对应边及对应角，再度量、计算，看看他们对应边的比有什么关系？对应角呢？

1．教师提供材料：请观察课本67页图18.2.1两张相似地图中的两个相似三角形ABC和三角形A₁B₁C₁

在丰富多彩的社会生活中，我们看到过许多相似的物体；在学习过程中也遇见不少相似图形。他们各有什么特征呢？如何识别他们相似呢？这都是我们今后要逐步探索学习的课题。这节课我们就来探索相似三角形。

在相似三角形概念形成的过程中，感受数学知识产生历程艘充满的探索性。

[重点难点]

重点：相似三角形概念和应用

难点：熟练地找出相似三角形中的对应元素；正确书写比例式

[教学准备]　

量角器、刻度尺、三角尺

[教学过程]

能运用相似三角形的概念解答一些简单的数学问题和实际问题；在运用过程中，培养有条理的思考和简单的推理能力。

经历相似三角形概念的形成过程，从而理解相似三角形概念；了解相似比概念，并据此理解相似三角形与全等三角形的区别和联系。

7.课外作业与拓展

参见励耘精品系列丛书《课时导航》华师大版八年级(下)P38－P39

6.回顾联系，形成结构

想一想:如何判断两个三角形相似？我们到现在为止共学了几种识别三角形相似的方法？

(通过问题的回答，引导学生自主总结，把分散的知识系统化、结构化，形成知识网络，完善学生的认知结构，加深对所学知识的理解．)

5.课内深化，提升能力

(1)依据下列各组条件,判定△ABC和△A′B′C′是否相似,并说明理由.

①AB=10cm,BC=8cm,AC=16cm, A′B′=16cm, B′C′=12.8cm, A′C′=25.6cm;

②∠A=80°, ∠C=60°, ∠A′=80°, ∠B′=40°;

③∠A=40°,AB=8,AC=15, ∠A′=40°, A′B′=16, A′C′=30.

(2)如图所示，，点C在△ABC的边DE上，∠1=∠2，AB：AC=AD：AE，试请说明：

△ABC∽△ADE；②∠B=∠D。

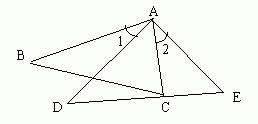
(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P39第16题)