
3.在射线OA、OB、OC、OD、OE上分别取点A′、B′、C′、D′、F′使OA′: OA= OB′:OB=OC′:OC=OD′:OD=OE′:OE=1.5
2.以O为端点作射线OA、OB、OC、OD、OE。
相似与轴对称、平移、旋转一样,是图形的一个基本变换。要把一个图形放大或缩小,又要保持其形状不变。就是要画相似图形,现在我们先从画相似多边形开始。
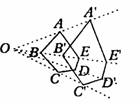 现在要把五边形ABCDE放大1.5倍,即是要画一个五边形A′B′C′D′E′,要与五边形ABCDE相似且相似比为1.5。
现在要把五边形ABCDE放大1.5倍,即是要画一个五边形A′B′C′D′E′,要与五边形ABCDE相似且相似比为1.5。
我们先考虑能否把五边形的一条边放大1.5倍呢?按照问题(2)中的作法,可以把AB放大1.5倍,同样也可以把其他边也放大,在平面上取一点O,以O为端点作射线OA、OB,可以画出线段A′B′,以此类推。
画法是:
1.在平面上任取一点O。
2.已知线段AB,画一线段A′B′,使A′B′=1.5AB,如何画呢?
画法有2:①延长AB至B′,使BB′=AB,②仿①直线外任取一点O,做射线OA,取AA′=AO.
1.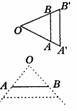 如图==,那么=?为什么?
如图==,那么=?为什么?
2、以O点为坐标原点建立平面直角坐标系,提出若AC=3,AO=1.写出A.B.C三点的坐标.
师生互动 问题1教师展示以后学生能很容易的解决,对于问题2教师要组织学生探究,并且与学生一同验证答案。
设计意图 上面的图形不仅含有相似三角形的有关知识,也是以后 学习“圆”中,经常出现的图形。因此要学生有一个深刻的印象,因此与学生一同巩固。
 问题2是提高学生综合运用知识的能力,也是对平面直角坐标系的巩固。
问题2是提高学生综合运用知识的能力,也是对平面直角坐标系的巩固。
㈢实际应用(17分钟)
教学内容 如图,△ABC是一 块木板余料,
边 AB=90厘米,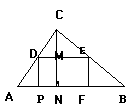 高CN=60厘米,要把它加工成正方形零 件,使正方形的一边在AB 上,其余两个顶点分别在BC、AC上, ①这个正方形零件的边长是多少?②如果把正方形的零件改变为加工矩形零件,设DP=x,DE=y,写出y与x之间的函数关系式,试确定x的取值范围。③当DE是DP的1.5倍时恰好符合要求,求此时零件的面积。④在问题3中,具体操作时,发现在AB线段上离B点34cm处有一蛀虫洞,请你确定一下,它是否影响余料的使用,说明理由。(量得BN=70cm)
高CN=60厘米,要把它加工成正方形零 件,使正方形的一边在AB 上,其余两个顶点分别在BC、AC上, ①这个正方形零件的边长是多少?②如果把正方形的零件改变为加工矩形零件,设DP=x,DE=y,写出y与x之间的函数关系式,试确定x的取值范围。③当DE是DP的1.5倍时恰好符合要求,求此时零件的面积。④在问题3中,具体操作时,发现在AB线段上离B点34cm处有一蛀虫洞,请你确定一下,它是否影响余料的使用,说明理由。(量得BN=70cm)
师生互动 对于问题1是曾经解决的问题,学生能独立完成,问题2需要教师与学生共同探究,使学生明 白它与1中应用的是同一知识。问题3教师组织学生独立完成即可。问题4教师要组织学生进行认真讨论,尽可能的使学生表述验证过程。教师做适当的补充。
设计意图 学以至用,实际问题有利于学生对所学知识的运用,在练习中还能有效的巩固学习的知识。2中的问题还训练学生综合运用知识的能力,4中的问题充分开发了学生的思维。
小结 相似三角形的识别方法与性质 (2分钟)
 课外拓展 右图中,在一直角三角形余料中截出一个面积最大的正方形零件,应如何截取? (设正方形的三边分别是3、4、5、那么最大的面积是多少?)
课外拓展 右图中,在一直角三角形余料中截出一个面积最大的正方形零件,应如何截取? (设正方形的三边分别是3、4、5、那么最大的面积是多少?)
设计意图 对学生掌握的内容进行拓展训练,也是对本节课涉及内容的一个 整体巩固巩固。
㈣板书设计


设计意图 使学生能清晰理解本章主要内容
《相似三角形(复习课)》教学设计(附课件)
王玉敏
满洲里市第二中学
2008年11月
教学设计内容:相似三角形(复习课)
版本: 华东师大版
章节: 八年级下册第18章《图形的相似》
教师简介:
王玉敏,女,1964年出生,中学一级教师。1983年9月参加工作。参加工作以后在内蒙古通辽师院进行函授学习,于1992年毕业。在工作的二十几年中一直进行初中数学教学,大部分时间从事班主任工作。工作中从各方面严格要求自己,努力提高自己的业务水平,丰富知识面,结合本校的实际条件和学生的实际情况,勤勤恳恳,兢兢业业,使教学工作有计划,有组织,有步骤地开展。二十几年的努力取得了骄人的业绩:1995年、1996年、2000年分别获得市级优秀辅导员称号,1999年、2006年在全国初中数学竞赛中获得优秀指导教师奖,2005年撰写的论文《初中数学新课程教学体会》获得自治区二等奖,同年撰写的论文《关于初中数学课程与信息技术整合的体会》获自治区电教论文三等奖。成绩属于过去,我会继续努力丰富自己,提高自己,为教育事业努力奋斗。 联系电话:15947109215
本人签名:
满洲里市第二中学
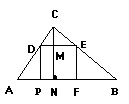
4. 在△ABC中AC=4,AB=5,.D是AC上一动点,且∠ADE=∠B,设AD=x,AE=y,写出y与x之间的函数关系式.试确定x的取值范围.
师生互动 问题1,2,3,教师组织学生独立完成,共同验证结论。第4个问题教师在学生探讨的基础上(没有正确解答),进行分解引导,提出引导问题:根据题中的条件,是否能得出图形相似;线段AC、AD、AB、AE之间具有怎样的关系?学生通过问题的分步理解,能较完整的解决问题。
设计意图 问题1、2、3,主要是通过不同的题型巩固相似三角形的性质,问题4主要是训练学生综合运用知识的能力,既巩固了相似三角形的性质又复习了一次函数的知识。同时这个问题还为下面一个实际问题奠定了基础。
|
教学内容 1、写出其中的几个等积式
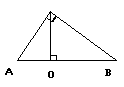
①AC2=
②BC2=
③OC2=
3.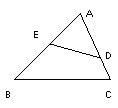 右图中, DE∥BC,S△ADE : S四边形DBCE = 1:8,则AE:AC=_____
右图中, DE∥BC,S△ADE : S四边形DBCE = 1:8,则AE:AC=_____
2.右图中,若D,E分别是AB,AC边上的中点,且DE=4则BC= _
1、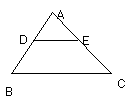 如图,点D、E分别是△ABC边AB、AC上
的点,且DE∥BC,BD=2AD,那么
如图,点D、E分别是△ABC边AB、AC上
的点,且DE∥BC,BD=2AD,那么
△ADE的周长︰△ABC的周长= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com