1.如图，已知五边形ABCDE，按相似比为3∶1，画出它的位似图形，使得位似中心位于：

①　　 位似中心为点A；

②　　 位似中心为线段AB的中点.

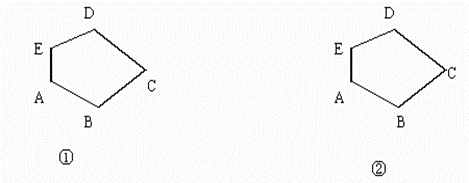
(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P41第4题)

4、练习反馈(5分钟内完成)

3、知识迁移

　　 利用位似的方法，可以把一个多边形放大或缩小.如图

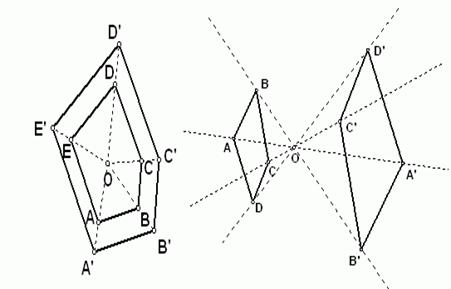
2、探索交流

例 画一个与五边形ABCDE相似的五边形AˊBˊCˊDˊEˊ，使新图形与原图形的相似比为1.5 .

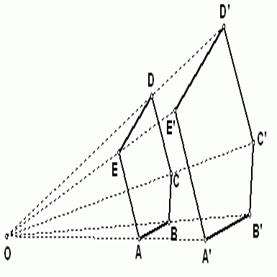
请同学们按照下面的步骤作图，教师协助同学完成.

　　 作法：(1)任取一点O；

　　　　 (2)以点O为端点作射线OA、OB、OC、OD、OE；

　　　　 (3)分别在射线OA、OB、OC、OD、OE上取点Aˊ、Bˊ、Cˊ、Dˊ、Eˊ，使OAˊ：OA = OBˊ：OB = OCˊ：OC =ODˊ：OD = OEˊ：OE = 1.5；

　　　　 (4)连结AˊBˊ、BˊCˊ、CˊDˊ、DˊEˊ、EˊAˊ得到所要画的五边形AˊBˊCˊDˊEˊ.

　　 做一做：用刻度尺和量角器量一量，看看上面的两个多边形是否相似？

归纳概括

　　 上面的两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的相似叫做位似 ( homothety ),点O叫做位似中心.

1、创设情景

相似形在生活中随处可见，画与一个图形相似的图形对我们来说就显得很重要.你能画一个与五边形ABCDE相似的五边形AˊBˊCˊDˊEˊ吗？

　　　　 让学生在实际应用中了解图形位似的概念，教材是通过画一个多边形相似的方法引入图形位似的概念，让学生能利用位似的方法，将一个图形放大或缩小，从而画出它的相似图形.相似与轴对称、 平移和旋转一样，也是图形之间的一个基本变换，可以将一个图形放大或缩小而保持形状不变.

P84　 习题18．4。

用位似法画相似的多边形，关键在于要确定位似中心，位似中心选在不同的位置，使画相似的过程的繁简也就不同。

任意画一个五边形，用位似法把它放大3倍。

4．连结A′B′，B′C′，D′E′，A′E′.

这样：＝＝＝＝＝1.5

再用量角器量它们的对应角，看看是否相等呢?

　　 也可以用平行线的性质推出各对应角是相等的，所以五边形A′B′C′D′E′就相似于五边形ABCDE。

　　 位似变换的定义：如上面的画法，两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的相似叫做位似。这点O叫做位似中心．放映电影时，胶片和屏幕上的画面就形成一种位似关系，它们的位似中心是放映机上的灯光的点。

　　 利用位似的方法，可以把一个多边形放大或缩小。

位似中心也可以取在多边形内，或多边形的一边上、或顶点，下面是位似中心不同的画法。

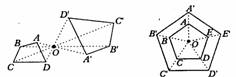
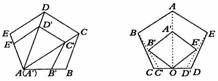
　　 在画相似多边形的过程中，同学们想一想，是否一定要取OA′: OA＝OB′:OB＝OC′:OC…，这样来取A′B′C′…这些点呢?如果我们只确定一个顶点A′后用其他方法来确定B′、C′……呢?