2.自变量的取值是x＞0．

上述两个函数都具有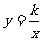的形式，一般地，形如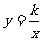(k是常数，k≠0)的函数叫做反比例函数(proportional function)．

说明 1.反比例函数与正比例函数定义相比较，本质上，正比例y＝kx，即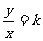，k是常数，且k≠0；反比例函数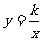，则xy＝k，k是常数，且k≠0．可利用定义判断两个量x和y满足哪一种比例关系．

1.当矩形的面积一定时，矩形的一边是另一边的反比例函数．即矩形的一边长增大了，则另一边减小；若一边减小了，则另一边增大；

2.自变量v的取值是v＞0．

问题2：学校课外生物小组的同学准备自己动手，用旧围栏建一个面积为24平方米的矩形饲养场．设它的一边长为x(米)，求另一边的长y(米)与x的函数关系式．

分析 根据矩形面积可知

　　　 xy＝24，

即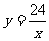　　

从这个关系中发现：

问题1 小华的爸爸早晨骑自行车带小华到15千米的镇外去赶集，回来时让小华乘公共汽车，用的时间少了．假设两人经过的路程一样，而且自行车和汽车的速度在行驶过程中都不变，爸爸要小华找出从家里到镇上的时间和乘坐不同交通工具的速度之间的关系．

分析 和其他实际问题一样，要探求两个变量之间的关系，就应先选用适当的符号表示变量，再根据题意列出相应的函数关系式．

设小华乘坐交通工具的速度是v千米/时，从家里到镇上的时间是t小时．因为在匀速运动中，时间＝路程÷速度，所以

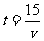
从这个关系式中发现:

1.路程一定时，时间t就是速度v的反比例函数．即速度增大了，时间变小；速度减小了，时间增大．

两个相关联的量，一个量变化，另一个量也随着变化，如果两个数的积一定，这两个数的关系叫做反比例关系．

5．一块长方形花圃，长为a米，宽为b米，面积为8平方米，那么a与b成_________函数关系，列出a关于b的函数关系式为___________________.

4．物体的质量不变时，其体积与密度成__________函数关系．

3．下面式子表示y是x的函数。

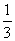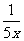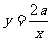　 (1)xy＝－；(2)y＝5一x；(3)y＝；(4) (a为常数且a≠0)．

其中__________是反比例函数．

2．下列各点中，在函数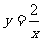图象上的点是　　 (　　 )

　　 A．(2，4)　　 B．(一1，2)　 C．(一2，一1)　 D．(一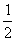，一1)

1．京沪高速公路全长约为1 262 km，汽车沿京沪高速公路从上海驶往北京，汽车行完全程所需的时间t (h)与行驶的平均速度v　 (km／h)之间有怎样的关系?变量t是v的反比例函数吗?答：____________________________________________-.