
上节的练习中,我们画出了问题1中函数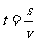 的图象,发现它并不是直线.那么它是怎么样的曲线呢?本节课,我们就来讨论一般的反比例函数
的图象,发现它并不是直线.那么它是怎么样的曲线呢?本节课,我们就来讨论一般的反比例函数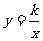 (k是常数,k≠0)的图象,探究它有什么性质.
(k是常数,k≠0)的图象,探究它有什么性质.
5.试用描点作图法画出问题1中函数的图象.
4.已知一个长方体的体积是100立方厘米,它的长是ycm,宽是5cm,高是xcm.
(1)写出用高表示长的函数式;
(2)写出自变量x的取值范围;
(3)当x=3cm时,求y的值.
3.已知y=y1+y2, y1与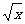 成正比例,y2与x2成反比例.当x=1时,y=-12;当x=4时,y=7.(1)求y与x的函数关系式和x的取范围;(2)当x=
成正比例,y2与x2成反比例.当x=1时,y=-12;当x=4时,y=7.(1)求y与x的函数关系式和x的取范围;(2)当x= 时,求y的值.
时,求y的值.
2.已知y与x-2成反比例,当x=4时,y=3,求当x=5时,y的值.
1.分别写出下列问题中两个变量间的函数关系式,指出哪些是正比例函数,哪些是反比例函数,哪些既不是正比例函数也不是反比例函数?
(1)小红一分钟可以制作2朵花,x分钟可以制作y朵花;
(2)体积为100cm3的长方体,高为hcm时,底面积为Scm2;
(3)用一根长50cm的铁丝弯成一个矩形,一边长为xcm时,面积为ycm2;
(4)小李接到对长为100米的管道进行检修的任务,设每天能完成10米,x天后剩下的未检修的管道长为y米.
本堂课,我们讨论了具有什么样的函数是反比例函数,一般地,形如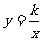 (k是常数,k≠0)的函数叫做反比例函数(proportional function).
(k是常数,k≠0)的函数叫做反比例函数(proportional function).
要求反比例函数的解析式,可通过待定系数法求出k值,即可确定.
例1 下列函数关系中,哪些是反比例函数?
(1)已知平行四边形的面积是12cm2,它的一边是acm,这边上的高是hcm,则a与h的函数关系;
(2)压强p一定时,压力F与受力面积s的关系;
(3)功是常数W时,力F与物体在力的方向上通过的距离s的函数关系.
(4)某乡粮食总产量为m吨,那么该乡每人平均拥有粮食y(吨)与该乡人口数x的函数关系式.
分析 确定函数是否为反比例函数,就是看它们的解析式经过整理后是否符合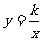 (k是常数,k≠0).所以此题必须先写出函数解析式,后解答.
(k是常数,k≠0).所以此题必须先写出函数解析式,后解答.
解 (1) ,是反比例函数;
,是反比例函数;
(2)F=ps,是正比例函数;
(3)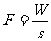 ,是反比例函数;
,是反比例函数;
(4)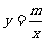 ,是反比例函数.
,是反比例函数.
例2 当m为何值时,函数 是反比例函数,并求出其函数解析式.
是反比例函数,并求出其函数解析式.
分析 由反比例函数的定义易求出m的值.
解 由反比例函数的定义可知:2m-2=1,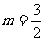 .
.
所以反比例函数的解析式为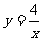 .
.
例3 将下列各题中y与x的函数关系与出来.
(1) ,z与x成正比例;
,z与x成正比例;
(2)y与z成反比例,z与3x成反比例;
(3)y与2z成反比例,z与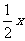 成正比例;
成正比例;
解 (1)根据题意,得z=kx(k≠0).
把z=kx代入 ,得
,得 ,即
,即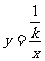 .因此y是x的反比例函数.
.因此y是x的反比例函数.
(2)根据题意,得 (k1,k2均不为0).
(k1,k2均不为0).
把 代入
代入 ,得
,得 ,即
,即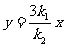 .
.
因此y是x的正比例函数.
(3)根据题意,得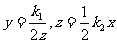 .把
.把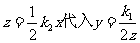 ,得
,得
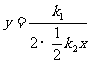 ,即y=
,即y=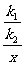 .因此y是x的反比例函数.
.因此y是x的反比例函数.
例4 已知y与x2成反比例,并且当x=3时,y=2.求x=1.5时y的值.
分析 因为y与 x2成反比例,所以设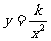 ,再用待定系数法就可以求出k,进而再求出y的值.
,再用待定系数法就可以求出k,进而再求出y的值.
解 设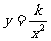 .因为当x=3时,y=2,所以
.因为当x=3时,y=2,所以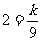 ,k =18.
,k =18.
当x=1.5时, .
.
例5 已知y=y1+y2, y1与x成正比例,y2与x2成反比例,且x=2与x=3时,y的值都等于19.求y与x间的函数关系式.
分析 y1与x成正比例,则y1=k1x,y2与x2成反比例,则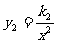 ,又由y=y1+y2,可知,
,又由y=y1+y2,可知,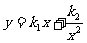 ,只要求出k1和k2即可求出y与x间的函数关系式.
,只要求出k1和k2即可求出y与x间的函数关系式.
解 因为y1与x成正比例,所以 y1=k1x;
因为y2与x2成反比例,所以 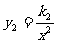 ,
,
而y=y1+y2,所以
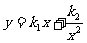 ,
,
当x=2与x=3时,y的值都等于19.
所以 解得
解得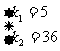
所以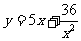 .
.
3.要求出反比例函数的解析式,只要求出k即可.
2.反比例函数的解析式又可以写成: ( k是常数,k≠0).
( k是常数,k≠0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com