2.将两个全等的不等边三角形拼成平行四边形，可拼成的不同的平行四边形的个数为______.

1.四边形ABCD中，对角线AC、BD相交于点O，要判别它是平行四边形，从四边形的角的关系看应满足______；从对角线看应满足_______.

11．如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=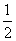BC．根据上面的结论：

　　 (1)你能否说出顺次连结任意四边形各边中点，可得到一个什么特殊四边形？并说明理由．

(2)如果将(1)中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”，那么它们的结论又分别怎样呢？请说明理由．

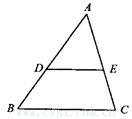
10．如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．

　　 (1)判断OE与OF的大小关系？并说明理由？

(2)当点O运动何处时，四边形AECF是矩形？并说出你的理由．

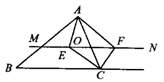
9．如图，一块正方形地板由全等的正方形瓷砖铺成，这地板的两条对角线上的瓷砖全是黑色，其余的瓷砖是白色的，如果有101块黑色瓷砖，那么瓷砖的总数是多少？

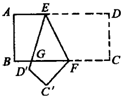
8．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D、C分别落在D′、C′的位置上，若∠EFG=55°，求∠AEG和∠ECB的度数．

7．在一个平行四边形中若一个角的平分线把一条边分成长是2cm和3cm的两条线段，求该平行四边形的周长是多少？

6．设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去……．

　　 (1)记正方形ABCD的边长为a₁=1，按上述方法所作的正方形的边长依次为a₂，a₃，a₄，……，a_n，请求出a₂，a₃，a₄的值．

(2)根据以上规律写出a_n的表达式．(8分)

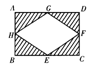
5．矩形，菱形由于其特殊的性质，为拼图提供了方便，因而墙面瓷砖一般设计为矩形，图案也以菱形居多．如图，是一种长30cm，宽20cm的矩形瓷砖，E、F、G、H分别是矩形各边的中点，阴影部分为淡黄色，中间部分为白色，现有一面长4.2m，宽2.8m的墙壁准备贴瓷砖．

　　 问：(1)这面墙壁最少要贴这种瓷砖多少块？

(2)全部贴满瓷砖后，这面墙壁最多会出现多少个面积相等的菱形？其中淡黄色的菱形有多少个？

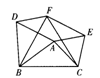
4．如图，以△ABC的各边向同侧作正△ABD，BCF，ACE．

(1)求证：四边形AEFD是平行四边形；

(2)当△ABC是_____三角形时，四边形AEFD是菱形；

(3)当∠BAC=_____时，四边形AEFD是矩形；

(4)当∠BAC=_______时，以A、E、F、D为顶点的四边形不存在．