3．进一步探求用两个独立的非同类条件判定平行四边形的方法．(这部分内容的设计意图和处理方法详见设计说明部分)

　　 (1)教师解释“两个独立的非同类条件”的含义，指从平行四边形四方面的性质(a)，(b)，(c)和(d)中各选取一个条件组合作为判定方法的题设部分，如一组对边平行((a)对边的位置关系)与一组对边相等((b)对边的数量关系)．

　　 (2)根据学生实际，让学生利用上述方法得出有关平行四边形判定方法的部分常用(或全部)猜想．(教师也可用判断题的形式让学生思考，从而降低难度)

　　 猜想一：一组对边平行且相等的四边形是平行四边形．

　　 猜想二：一组对边平行且另一组对边相等的四边形是平行四边形．

猜想三：一组对边相等且一组对角相等的四边形是平行四边形．

　猜想四：一组对边平行且一条对角线被另一条对角线平分的四边形是平行四边形．(其他猜想见设计说明中的补充内容)

　　 (3)证明猜想成立或举例说明某猜想不成立．

以上猜想中正确的是猜想一和四，猜想二和三的反例图形分别见图

4-21(a)，(b)．

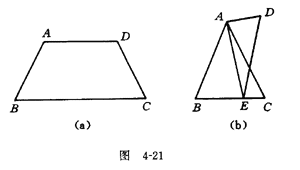
　　 如图4－21(a)，在四边形ABCD中， AD //BC，　 AB＝DC，但四边形ABCD不是平行四边形；在图4-21(b)中， AB＝AC＝DE，∠B=∠C＝∠D，但四边形 ABED不是平行四边形．

　 (4)将正确的命题中作用较大的猜想一作为判定定理4使用，其余的命题让学生熟悉结论和研究方法．

　(5)总结。平行四边形共有五种判定方法，根据题目条件从中灵活选用方法来解决问题．

2．逆向思维：怎样判定一个四边形是平行四边形？

　　 (1)学生容易由定义得出：两组对边分别平行的四边形是平行四边形(判定方法一)．也就是说，定义既是平行四边形的一个性质，又是它的一个判定方法．

　　 (2)观察判定方法一与性质1的关系，寻找逆命题的特征：

　　 ①由两个独立条件和一个结论组成；

　　 ②两个独立条件属于同类条件(即都分别属于：(a)对边的位置关系，(b)对边的数量关系，(c)对角的数量关系或(d)对角线关系的条件，简称为同类条件)；

　　 ③逆命题正确．

　　 (3)类比联想，猜想其他性质的逆命题也能判定平行四边形，构造逆命题如下：

　　 ①两组对边分别相等的四边形是平行四边形(猜想1)；

　　 ②两组对角分别相等的四边形是平行四边形(猜想2)；

　　 ③对角线互相平分的四边形是平行四边形(猜想3)．

　　 (4)证明猜想，得到平行四边形的判定定理1，2，3．

　　 教师引导学生根据平行四边形的定义以及平行线的性质、三角形全等的知识对以上猜想

进行证明．

　　 注意利用新证定理简化后来读定理的证明过程及选择简捷方法．

引导学生观察、发现，激发学生的好奇心和求知欲，并且引导学生在应用数学知识解决实际问题的活动中体验成功，树立学习的自信心。

[教学重点]：平行四边形的性质的探究和应用

[教学难点]：平行四边形的性质的探究

[教学方法]：

按照学生的认知规律，遵循教师为主导，学生为主体，训练为主线的指导思想，采用观察发现法为主，多媒体演示法为辅。教学中，设计启发性思考问题，创设问题情境，引导学生思考。教学适时运用电教媒体化静为动，激发学生探求知识的欲望，逐步推导归纳得出结论，使学生始终处于主动探索问题的积极状态

[教学过程]：

活动1：

展示含有平行四边形模型的图片，并找出平行四边形的原形，从而回顾平行四边形的定义，让学生在感受美的同时，体会数学源于生活，激发学生学习的兴趣，并由此引入课题：平行四边形的性质。

活动2：

体现从实践出发，我让学生用两张平行的纸条叠在一起旋转，观察AD BC 角ABC　 ADC的大小关系？“他们都在动，这么比较大小呢？”面对学生的困惑我不急于回答，而且把话锋一转，让学生按照平行四边形定义画一个平行四边形，中间观察多数同学的作图情况，安排用课件演示平行四边形作图全过程，学生分组合作，引导学生观察 猜想 度量所画平行四边行对边，对角的大小关系，并填写好实验报告，接着让学生剪下所画四边形，帖在白纸上，以原四边形为模型再从新话一个四边形，然后固定对角线交点O，旋转一个180度，观察对角线OA OB OC OD 的位置关系，和大小关系，并填写实验报告。鼓励学生大胆猜想，培养学生抽象概括能力和语言表达能力。

活动3：

验证猜想，并为后面证明铺路，让学生用全等或不全等的两个三角形拼成一个平行四边形，学生动手实验，只能用两个全等三角形来拼，等学生做完后，我抓住时机提问“通过动手实验你受到了什么启示，你能证明你刚才的猜想吗？”这时有的同学抓头挠耳，跃跃欲试，在我的引导下分析命题的条件和结论，用几何语言写出“已知、求证”，并画出图形。让学生分组合作，巡视之后利用实物投影展示部分学生的证明方法，并由学生进行讲评。最后，在多媒体给出规范的证明方法。这一过程不仅培养了学生的合作精神，又体现由特殊到一般的思维认识规律，突出重点，同时也展示了先猜想、后证明这一数学认知基本方法。

活动4：

为进一步深化巩固对新知的理解，使新知识转化成技能，我安排了以下例题。

沙市二中的前身是创办于20世纪初的晴川书院，1953年改制为沙市第二中学，沿用至今，已有百年的校史，随着一代又一代的晴川人艰苦卓越的耕耘，如今的沙市二中逐渐成为了驰名荆楚大地的质量强校。2008年，在市政府的统筹规划下，学校由便河广场喜迁至美丽的江津湖畔。因此，有很多同学需要乘公交上学，小明所在街道如图所示，AF垂直平分CE，AB∥CD，CB∥AD，小明从家(A)到学校(F)有两路公交车，19路：A　 B　 C　　 F　 ；4路：A　 D　 E　　 F，那条路最短？为什么？

通过例题教学，突出本节重点,加深对平行四边形定义及性质的理解,培养学生分析、解决实际问题的能力，通过例题的变式，由浅入深分层训练，让学生轻松完成例题的学习，达到对知识的掌握。

活动5：

　1﹑已知:如图(1)　　 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点PQ,求证:MQ=NP

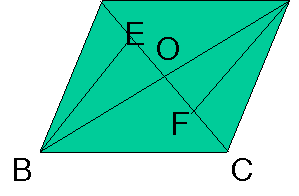
2.已知如下图，在平行四边行ABCD中，AC与BD相交于点O，点E、F在AC上，且BE∥DF。

活动6：

平行四边形ABCD中E在AD上，以BE为折痕,将△ABE向上翻折,A点刚好落在CD上点F,若△FDE的周长为8, △FCB的周长为22,求FC的长度?

活动7：

为了使学生对所学知识有一个完整而深刻的认识，我让学生畅所欲言，谈收获，谈体会，让学生自已发现在学习中学会了什么及还存在哪些问题。这样有利于学生养成学习后及时反思的习惯。

课后作业我分为必做题和选做题，必做题比较简单，要求全做，选做题较难，要求学有余力的学生完成。作业体现分层教学，因材施教原则，目的是进一步提高学生解决问题能力，培养学生学数学，用数学的意识。

本课板书，我分为三个板块，力求板面整齐有序，“一板清”，勾勒出教学的主线，呈现完整的知识结构体系，并突出重点，便于学生掌握。

在本节课的教学设计中,注重对数学学习兴趣的培养,通过学生动手实践，观察分析，猜想证明，引导学生完成了从感性认识到理性认识的认知，最后运用所学知识解决问题，突现应用意识和创新意识。在教学过程中，强调学生形成积极主动的学习态度，关注学生的学习兴趣和体验，充分体现“数学教学是数学活动的教学”这一教育思想。

在性质的探索、发现与证明的过程中，培养学生的观察能力及逻辑推理论证能力，渗透“转化”的数学思想。

理解平行四边形的定义，掌握平行四边形的有关性质，并能初步应用平行四边形的性质进行简单的计算和证明，解决生活中的实际问题。

10.是平行四边形,△AOE≌△COF.

11是平行四边形，四边形AMCN、BMDN是平行四边形.

9. 线段AC与EF互相平分.理由是：∵四边形ABCD是平行四边形.

∴AB∥CD,即AE∥CF，AB=CD，∵BE=DF，∴AE=CF

∴四边形AECF是平行四边形，

∴AC与EF互相平分.

8.证明：(1)∵BD=CD，∴∠BCD=∠1．∵ ∠l=∠2，∠BCD=∠2．∴CD∥AB．

　　 (2) ∵ CD∥AB　 ∴∠CDA=∠3．

　　　 ∠BCD=∠2=∠3．且BE=AE．且∠CDA=∠BCD．∴DE=CE．

　　　 在△BDE和△ACE中， DE=CE，∠DEB=∠CEA，BE=AE．∴△BDE≌△ACE

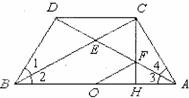　　 (3) ∵△BDE≌△ACE

　　　 ∠4=∠1，∠ACE=∠BDE=90°．

∴∠ACH=90°一∠BCH

　　　 又CH⊥AB，．∴ ∠2=90°一∠BCH

∴∠ACH=∠2=∠1=∠4．AF=CF

∵∠AEC=90°一∠4，∠ECF=90°一∠ACH

　　　 ∠ACH=∠4 ∠AEC=∠ECF．CF=EF．∴ EF=AF

　　　 O为AB中点，OF为△ABE的中位线　　 ∴OF=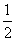BE

7.解：∵BA∥DE，BD∥AE，∴四边形ABDE是平行四边形

∴AB=DE，BD=AE，又EF=FC且AF∥BC，EC⊥BC，∴DE=DC，

∴EA+AE+EF=BD+DC+CF，∴二人同时到达F站.