
2.从分类的角度来看,用非同类条件判定平行四边形的猜想,还有以下几种,教师可根情况选用.
猜想五:一组对边平行且一组对角相等的四边形是平行四边形.
猜想六:一组对边相等,对角线交点平分其中某一条对角线的四边形是平行四边形
 .
.
猜想七:一组对角相等,连该对角的两顶点的对角线平分另一条对角线的四边形是平边形.
猜想八:一组对角相等,连该对角的两顶点的对角线被另一条对角线平分的四边形是平行四边形.
其中猜想六,八是假命题,猜想五,七是真命题,可由学生课下加以证明,其中猜想七的证明需要用到圆的知识.
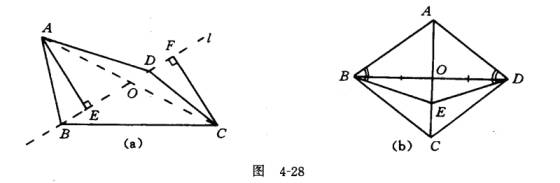
猜想六,八的反例图形分别是图428(a),(b).
缺图4-28
如图 4-28(a),AE⊥l,CF⊥l,AE=CF,BE=DF,OE=OF,则四边形ABCD中,AB=DC,AO=OC,但四边形ABCD不是平行四边形。
如图4-28(b),菱形ABCD中,E为对角线AC上一点,则四边形ABED中,∠ABE=∠ADE,BO=OD.但四边形ABCD不是平行四边形.
1.由平行四边形的定义及性质定理逆向探索它的判定方法,是以后经常用到的思考方
法.因此,教师应让学生明确建立这种意识,并尽量独立完成这个过程.
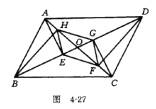
3.如图4-27,在 ABCD中,AC,BD交于O点,AE⊥BD于E,CG⊥BD于G,BH⊥
ABCD中,AC,BD交于O点,AE⊥BD于E,CG⊥BD于G,BH⊥
AC于H,DF⊥AC于F.求证:四边形EFGH为平行四边形.
课堂教学设计说明
本教学设计需2课时完成.
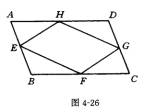
2.如图4-26,在 ABCD中,E,F,G和H分别是各边中点.求证:四边形EFGH为平行四边形.
ABCD中,E,F,G和H分别是各边中点.求证:四边形EFGH为平行四边形.

课本第144页第7-14题,B组1,2,4题.
补充题:
1.如图 4-25,在 ABCD中, AE=CF, BG=DH.求证: AH,BE,CG,DF围成的四边形
ABCD中, AE=CF, BG=DH.求证: AH,BE,CG,DF围成的四边形
MNPQ为平行四边形.
3.学习了哪些研究问题的思想方法?
2.怎样来画符合条件的平行四边形?
1.平行四边形的判定方法有哪些?应从边、角、对角线三方面来进行总结,并指出:性质定理的逆命题如果正确,常常作为判定定理来使用.
2.画出符合条件的平行四边形.
例 3画 ABCD,使∠B=45°, AB=2cm, BC=3cm.
ABCD,使∠B=45°, AB=2cm, BC=3cm.
分析:
(1)画平行四边形的关键是先由条件确定平行四边形中三个顶点所组成的三角形,例如,此题可根据“两邻边及一夹角”先确定△ABC.
(2)可根据平行四边形的五种判定方法来确定平行四边形的第四个顶点.但其中根据判定定理1作图较为复杂,一般不常用.
让学生画图,并写出画法.
练习课本第140页第1,2题,第142页第1,2,3题.
1.利用平行四边形的判定定理及性质定理进行证明.
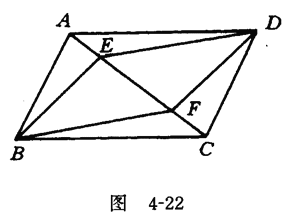
例1已知:如图 4-22,E和F是 ABCD对角钱AC上两点,AE=CF.求证:四边形BFDE是平行四边形.
ABCD对角钱AC上两点,AE=CF.求证:四边形BFDE是平行四边形.
分析:可使用五种判定方法来证明这个结论,其中“添加对角线构造使用判定定理3的条件”的证明方法最为简捷.
说明:引导学生从条件、结论两方面对题目进行再思考.
(1)在此基础上,还可证出什么结论?用到什么方法?如还可证BE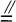 DF,DE
DF,DE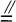 BF, ∠BED=∠BFD等.总结方法:利用平行四边形的性质--判定--性质可解决较复杂的几何题目.
BF, ∠BED=∠BFD等.总结方法:利用平行四边形的性质--判定--性质可解决较复杂的几何题目.
(2)根据运动、类比、特殊化的思维方法,猜想对此题可作怎样的推广?
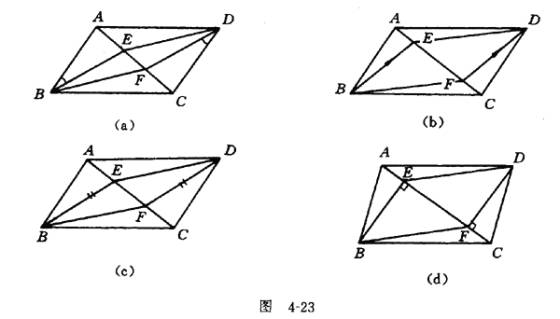
类比例1条件,利用运动变化的观点,让E和F在对角线AC上运动到一些特殊位置,猜想还可得出同样结论如图4-23,但其中的猜想无法证明.
缺图4-23
猜想一如图 4-23(a),在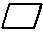 ABCD中, E,F为AC上两点,∠ABE=∠CDF.求证:四边形BEDF为平行四边形.
ABCD中, E,F为AC上两点,∠ABE=∠CDF.求证:四边形BEDF为平行四边形.
猜想二如图4-23(b),在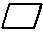 ABCD中,E,F为AC上两点,BE//DF.求证:四边形BEDF为平行四边形.
ABCD中,E,F为AC上两点,BE//DF.求证:四边形BEDF为平行四边形.
猜想三如图 4-23(c),在 ABCD中, E,F为AC上两点, BE=DF.求证:四边形 BEDF为平行四边形.
ABCD中, E,F为AC上两点, BE=DF.求证:四边形 BEDF为平行四边形.
猜想四如图4-23(d),在 ABCD中,E,F分别是AC上两点,BE⊥AC于E,DF⊥AC于F.求证:四边形
ABCD中,E,F分别是AC上两点,BE⊥AC于E,DF⊥AC于F.求证:四边形 BEDF为平行四边形
BEDF为平行四边形
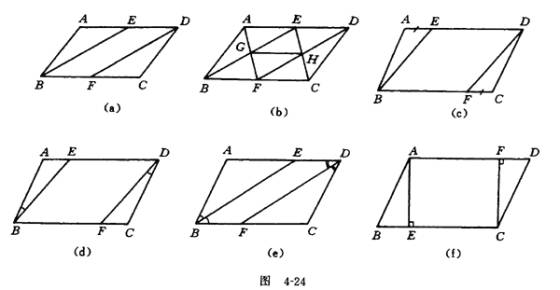
例2已知:如图 4-24(a),在 ABCD中,E,F分别是边AD,BC的中点.求证:EB=DF.
ABCD中,E,F分别是边AD,BC的中点.求证:EB=DF.
说明:
(1)分析证明思路,所要证明的两条线段恰为四边形EBFD的一组对边,由图中它们所在的位置来看,可首先判定四边形BEDF为平行四边形,再利用平行四边形的性质来解决.培养学生思维的层次:使用已知平行四边形的性质--判定新平行四边形--使用新平行四边形的性质得出结论.
(2)引导学生适当改变题目的条件、结论,对命题加以引伸和推广.
推广一(对结论引伸)已知:如图4-42(b),在 ABCD中,E,F分别为AD,BC的中点,
ABCD中,E,F分别为AD,BC的中点,
BE交AF于G,EC交DF于H.求证:
(1)四边形EGFH为平行四边形;
(2)四边形EGHD为平行四边形.
思考:怎样用运动、类比及特殊到一般的方法来改变命题的条件,将命题加以推广?
推广二已知:如图 4-24(c),在 ABCD中,E, F为AD,BC上两点,AE=CF.求证:EB=DF.
ABCD中,E, F为AD,BC上两点,AE=CF.求证:EB=DF.
推广三已知:如图 4-24( d),在 ABCD中, E, F为 AD,BC上两点,∠ABE=∠ CDF.
ABCD中, E, F为 AD,BC上两点,∠ABE=∠ CDF.
求证:EB= DF.
推广四已知:如图4-24(e),在 ABCD中,E,F分别为AD,BC上两点,BE和DF分
ABCD中,E,F分别为AD,BC上两点,BE和DF分
别平分∠ABC和∠ADC.求证:EB= DF.
推广五已知:如图4-24(f),在 ABCD中,E,F分别为AD,BC上两点,AE⊥BC于
ABCD中,E,F分别为AD,BC上两点,AE⊥BC于
E, CF⊥AD于F.求证:BE=DF.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com