3．对角线的关系：证明两条对角线互相平分．

　　 备注：借助图形来理解，总结．

2．角的关系：证明两组对角分别相等．

　　 平行四边形判定：

1．边的关系：

1．课本P97“练习”　 1，2．

　　 例3(投影显示)

如图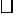，ABCD的对角线AC，BD交于点O，E、F是AC上的两点，并且AE=CF．求证四边形BFDE是平行四边形．

　　 思路点拨：例3的证明方法有多种，思路1：用课本的证法，依据平行四边形的对角线性质为方向，用AE=CF，可得OE=OF，OB=OD，从而得证．思路2：连接BE、DF，利用三角形全等来证明四边形BFDE的两组对边分别相等．思路3：证明△ADE≌△BCF得到DE=BF，∠DEO=∠BFO．从而推出DE∥BF，也就是说用一组对边平行且相等的方法来证．但课本的证法最简单．

　　 教师活动：操作投影仪，分析例3，引导学生从不同的思路来证明例3．拓宽学生的思维，请部分学生上讲台演示．

　　 学生活动：分四人小组，合作交流，对例3提出不同的证明思路．踊跃上台“板演”．

　　 [设计意图]以例3为素材，发展学生一题多证的发散性思维，同时将上面的三种平行四边形的判定方法进行应用、归纳，形成切入点，但要注意采用最优证法．

　　 [课堂演练](投影显示)

演练题：在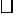ABCD中，E、F分别是AB、CD的中点，四边形AECF是平行四边形吗？证明你的结论．

　　 思路点拨：本道题有多种证法，如：可以从一组对边平行且相等的角度切入去证AE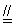FC；也可以从两组对边分别相等的切入点予以证明，去证AE=FC，AF=EC．

　　 [活动方略]

　　 教师活动：操作投影仪，组织学生训练，巡视、关注“学困生”的思维，发现好的证明方法．

　　 学生活动：独立思考，应用所学知识切入进行证明，形成分析思路，注意问题转化．踊跃上台演示．

　　 教师活动：在学生充分思考的基础上，请几位不同证明方法的学生上讲台演示，同时纠正书写表达方法．

　　 评析：应用一组对边平行且相等的方法较为简捷，在分析中要善于将未知问题逆推转化成能够解决的熟悉问题．

　　 [设计意图]让学生反复认识，学会分析．

2．平行四边形性质是什么？如何概括？

　　 学生活动：思考后举手回答：

回答：1．两组对边分别平行的四边形叫做平行四边形(教师在黑板上画出下图：帮助学生直观理解)

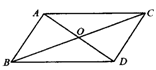
　　 回答：2．平行四边形性质从边考虑：(1)对边平行，(2)对边相等，(3)对边平行且相等(“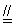”)；从角考虑：对角相等；从对角线考虑：两条对角线互相平分．(借助上图直观理解)．

　　 教师归纳：(投影显示)

　　 平行四边形

　　 [活动方略]

　　 教师活动：操作投影仪，显示课本P96和P97“探究”的问题．用问题牵引学生动手操作、思考、发现、归纳、论证，可以让学生分成4人小组讨论，然后再进行小组汇报，教师同时也拿出教具同学在一起探索．

学生活动：分四人小组，拿出准备好的学具探究．在活动中发现：(1)将两长两短的四根细木条(或用硬纸片)，用小钉铰合在一起，做成四边形，如果等长的木条成对边，那么无论如何转动这四边形，它的形状都是平行四边形；(2)若将两根细木条中点用钉子钉合在一起，用像皮筋连接木条的顶点，做成一个四边形，转动两根木条，这个四边形是平行四边形．(3)将两条等长的木条平行放置，另外用两根木条(不一定等长)用钉子予以加固，得到的四边形一定是平行四边形．(如下图)

　　 教师活动：归纳学生的发言，将问题引入到平行四边形判定方法上来．

　　 教师归纳：(借助上面的性质归纳)

平行四边形判定与性质：

　　 备注：具体内容见课本P96-P97，教师此时可引导学生对定理进行证明．

　　 提出问题：同学们能否证明出上面所提出的判定呢？

　　 学生活动：开始证明上面提出的判定方法．主要是通过辅助线将四边形切割成一对三角形，再证明这对三角形全等把问题归结到定义上去．

　　 评析：在教师的指导下，学生学会添加辅助线，并学会数学的化归思想，这是几何学的重要环节，应予以突破．

　　 [设计意图]将两个“探究”应用操作感知的方法来发现，再应用数学化归思想，借助辅助线予以推理论证，达到解决重点，突破难点的目的．

　　 教师提问：

1．平行四边形定义是什么？如何表示？

10．(2002年福州市中考题)如图，已知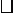ABCD的对角线AC、BD相交于点O，EF过点O，且与BC、AD分别相交于点E、F，求证：OE=OF．

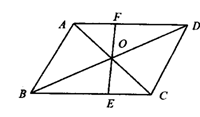
9．(2004年江苏省南京市中考题)如图，E、F是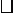ABCD的对角线AC上的两点，AE=CF．

　　 求证：(1)△ABE≌△CDF；

　　　　 (2)BE∥DF．