
2.选用课时作业优化设计
1.课本P100-102 习题19.1 7,8,13,14
3.利用三角形中位线定理,添加辅助线的方法有:
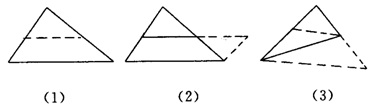
2.把握三角形中位线定理的应用时机:
(1)题目的条件中出现两个或两个以上的线段中点;
(2)题目的条件中虽然只有一个(线段的)中点,但过这点有直线平行于过中点所属线段端点的直线.
1.三角形中位线定理:三角形两边中点的连线是三角形的中位线;三角形的中位线平行于第三边,并且等于第三边的一半.三角形的中位线是三角形中一条重要的线段,三角形中位线定理在许多计算及证明中都要用到.
2.[探研时空]
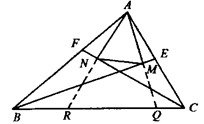
如图,已知BE、CF分别为△ABC中∠B、∠C的平分线,AM⊥BE于M,AN⊥CF于N,求证:MN∥BC.
(提示:延长AN,AM,证AN=NR,AM=MQ.利用三角形中位线定理可证).
1.课本P99 “练习”1,2,3.
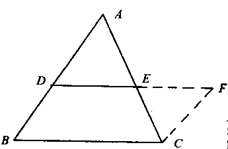
例4 如图,点D,E分别是△ABC的边AB、AC的中点,求证DE∥BC,且DE=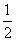 BC.
BC.
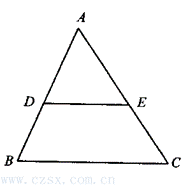
思路点拨:对于证明某条线段是某条线段的一半,常用的几何方法是“加倍法”,“折半法”,通过三角形全等把问题化归到平行四边形问题中去,然后再利用平行四边形的有关概念、性质来解决.本题可以延长DE到F,使EF=DE,通过连结AF、FC、CD把问题转化到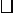 ADCF中去,再根据平行四边形性质证明
ADCF中去,再根据平行四边形性质证明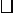 DBCF.
DBCF.
[活动方略]
教师活动:板书例4,分析并引导学生积极参与.教会学生如何添加辅助线,如何书写辅助线的添加法,然后板书出例4的证明.
学生活动:参与教师分析例4,学会“加倍法”的几何分析思路.
教师板书例4证法:(见课本P98)
教师问题:还有没有不同于课本的证法呢?
学生活动:相互讨论,踊跃发言,想出不同的证法.上讲台演示.
参考证法:
证法:延长DE到F使得EF=DE,连结FC,证△ADE≌△FEC,得到AD=FC(割补法),再利用BDCF证出DB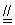 CF,从而得到DF=BC,推出DE=
CF,从而得到DF=BC,推出DE=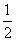 BC,DE∥BC.
BC,DE∥BC.
能用折半法吗?试一试!
教师活动:归纳学生的不同证法,然后应用例4的结论导入新知:(口述后让学生翻开课本画一画).
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:三角形中位线平行于三角形的第三边,且等于第三边的一半.
教师提问:一个三角形有几条中位线?中位线和三角形的中线一样吗?
学生回答:有三条中位线,中位线是两边中点连线段;而中线是顶点和对边中点的连线段,因此它们不同.
[设计意图]采用引例导入,丰富学生的联想,又能从中学会几何不同的证明方法.
3.平行四边形是如何判定的?
教师板书:画出一个平行四边形,如下图.(帮助理解)
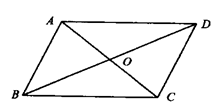
学生活动:踊跃发言,相互讨论,归纳出平行四边形的性质与判定.
[课堂演练](教师板书)
演练题:如图,平行四边形ABCD中,对角线AC、BD相交于O,E、F分别为BO、DO的中点.求证:AF∥CE.(请你用两种方法证明)
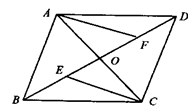
思路点拨:方法1:证明△AOF≌△COE,推出∠AFE=∠CEF,从而得证AF∥CE.方法2:连结AE,CF,去证明四边形AECF为平行四边形.
教师活动:组织学生完成“演练题”,巡视、关注“学困生”,对于思路较好的学生,请他们完成后再上台演示.教师注意纠正他们的书写.
学生活动:独立完成“演练题”,结合本道题,回顾和应用平行四边形性质,判定.
[师生共识]
构图:
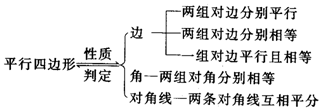
[设计意图]采用先回顾(提问式)平行四边形性质、判定,再通过“演练题”进行实际应用,这样不空洞,且能调动积极性,有利于归纳、提升.
[课堂温习]
教师提问:1.平行四边形的定义是什么?
2.平行四边形具有哪些性质?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com