
19.1.2 平行四边形的判定(三)
|
教学目标 |
知识与技能 |
1.
理解三角形中位线的概念,掌握它的性质. 2. 能较熟练地应用三角形中位线性质进行有关的证明和计算. |
|
过程与方法 |
经历探索、猜想、证明的过程,进一步发展推理论证的能力.感悟几何学的推理方法. |
|
|
情感态度与价值观 |
培养学生合情推理意识,形成几何思维分析思路,体会几何学在日常生活中的应用价值. |
|
|
重点 |
掌握和运用三角形中位线的性质. |
|
|
难点 |
三角形中位线性质的证明(辅助线的添加方法) |
教 学 过 程
|
备 注 |
教学设计 与 师生互动 |
|
|
第一步:课堂引入 1. 平行四边形的性质;平行四边形的判定;它们之间有什么联系? 2. 你能说说平行四边形性质与判定的用途吗? (答:平行四边形知识的运用包括三个方面:一是直接运用平行四边形的性质去解决某些问题.例如求角的度数,线段的长度,证明角相等或线段相等等;二是判定一个四边形是平行四边形,从而判定直线平行等;三是先判定一个四边形是平行四边形,然后再眼再用平行四边形的性质去解决某些问题.)  实验:请同学们思考:将任意一个三角形分成四个全等的三角形,你是如何切割的?(答案如图) 实验:请同学们思考:将任意一个三角形分成四个全等的三角形,你是如何切割的?(答案如图)图中有几个平行四边形?你是如何判断的? |
第二步: 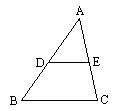 引入新课 引入新课 例(教材P98例4) 如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE= 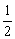 BC. BC.分析:所证明的结论既有平行关系,又有数量关系,联想已学过的知识,可以把要证明的内容转化到一个平行四边形中,利用平行四边形的对边平行且相等的性质来证明结论成立,从而使问题得到解决,这就需要添加适当的辅助线来构造平行四边形. 方法1:如图(1),延长DE到F,使EF=DE,连接CF,由△ADE≌△CFE,可得AD∥FC,且AD=FC,因此有BD∥FC,BD=FC,所以四边形BCFD是平行四边形.所以DF∥BC,DF=BC,因为DE= 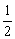 DF,所以DE∥BC且DE= DF,所以DE∥BC且DE=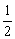 BC. BC.(也可以过点C作CF∥AB交DE的延长线于F点,证明方法与上面大体相同)  方法2:如图(2),延长DE到F,使EF=DE,连接CF、CD和AF,又AE=EC,所以四边形ADCF是平行四边形.所以AD∥FC,且AD=FC.因为AD=BD,所以BD∥FC,且BD=FC.所以四边形ADCF是平行四边形.所以DF∥BC,且DF=BC,因为DE= 方法2:如图(2),延长DE到F,使EF=DE,连接CF、CD和AF,又AE=EC,所以四边形ADCF是平行四边形.所以AD∥FC,且AD=FC.因为AD=BD,所以BD∥FC,且BD=FC.所以四边形ADCF是平行四边形.所以DF∥BC,且DF=BC,因为DE=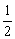 DF,所以DE∥BC且DE= DF,所以DE∥BC且DE=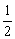 BC. BC.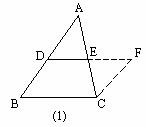 三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线 三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线[思考]: (1)想一想:①一个三角形的中位线共有几条?②三角形的中位线与中线有什么区别? (2)三角形的中位线与第三边有怎样的关系? (答:(1)一个三角形的中位线共有三条;三角形的中位线与中线的区别主要是线段的端点不同.中位线是中点与中点的连线;中线是顶点与对边中点的连线. (2)三角形的中位线与第三边的关系:三角形的中位线平行与第三边,且等于第三边的一半.) 三角形中位线的性质:三角形的中位线平行与第三边,且等于第三边的一半. [拓展]利用这一定理,你能证明出在设情境中分割出来的四个小三角形全等吗?(让学生口述理由) |
|
第三步:应用举例 例1已知:如图(1),在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点. 例1已知:如图(1),在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. 分析:因为已知点E、F、G、H分别是线段的中点,可以设法应用三角形中位线性质找到四边形EFGH的边之间的关系.由于四边形的对角线可以把四边形分成两个三角形,所以添加辅助线,连接AC或BD,构造“三角形中位线”的基本图形后,此题便可得证. 证明:连结AC(图(2)),△DAG中, ∵ AH=HD,CG=GD, ∴ HG∥AC,HG= 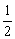 AC(三角形中位线性质). AC(三角形中位线性质).同理EF∥AC,EF= 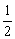 AC. AC.∴ HG∥EF,且HG=EF. ∴ 四边形EFGH是平行四边形.  此题可得结论:顺次连结四边形四条边的中点,所得的四边形是平行四边形. 此题可得结论:顺次连结四边形四条边的中点,所得的四边形是平行四边形. |
|
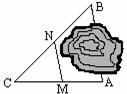 第四步:课堂练习 第四步:课堂练习1.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20 m,那么A、B两点的距离是 m,理由是 . 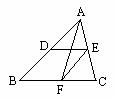 2.已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长. 2.已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长.3.如图,△ABC中,D、E、F分别是AB、AC、BC的中点, (1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm; (2)中线AF与DE中位线有什么特殊的关系?证明你的猜想. |
|
|
第五步:课后巩固 1.(填空)一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是 cm. 2.(填空)已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是 cm. 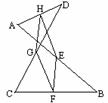 3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. 3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形. |
|
|
课后小结与反思 : |
19.1.2 平行四边形的判定(一)
|
教学目标 |
知识与技能 |
1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法. 2.会综合运用平行四边形的判定方法和性质来解决问题. 3.培养用类比、逆向联想及运动的思维方法来研究问题. |
|
过程与方法 |
经历平行四边形判定条件的探索过程,发展学生的合情推理意识和表述能力. |
|
|
情感态度与价值观 |
培养学生合情推理能力,经及严谨的书写表达,体会几何思维的真正内涵. |
|
|
重点 |
理解和掌握平行四边形的判定定理. |
|
|
难点 |
几何推理方法的应用. |
教 学 过 程
|
备 注 |
教学设计 与 师生互动 |
|
|
第一步:创景引入: 老师提问: 1、平行四边形定义是什么?如何表示? 2、平行四边形性质是什么?如何概括? 演示图片:选择各种四边形图片展示. 提出问题,在刚才演示的图片中,有哪些是平行四边形?你是怎样判断的? [探究]:小明的父亲手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗? 请学生通过观察、测量、猜想、验证、探索构成平行四边形的条件,思考并探讨: (1)你能适当选择手中的硬纸板条搭建一个平行四边形吗? (2)你怎样验证你搭建的四边形一定是平行四边形? (3)你能说出你的做法及其道理吗? (4)能否将你的探索结论作为平行四边形的一种判别方法?你能用文字语言表述出来吗? (5)你还能找出其他方法吗? 总结: 平行四边形判定1 两组对边分别相等的四边形是平行四边形. 平行四边形判定2 对角线互相平分的四边形是平行四边形. |
第二步:应用举例: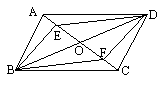 例1(教材P96例3)已知:如图 例1(教材P96例3)已知:如图 ABCD的对角线AC、BD交于点O,E、F是AC上的两点,并且AE=CF. ABCD的对角线AC、BD交于点O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 分析:欲证四边形BFDE是平行四边形可以根据判定方法2来证明. (证明过程参看教材) 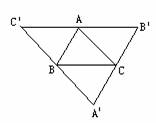 问;你还有其它的证明方法吗?比较一下,哪种证明方法简单. 问;你还有其它的证明方法吗?比较一下,哪种证明方法简单.例2(补充) 已知:如图,A′B′∥BA,B′C′∥CB, C′A′∥AC. 求证:(1) ∠ABC=∠B′,∠CAB=∠A′,∠BCA=∠C′; (2) △ABC的顶点分别是△B′C′A′各边的中点. 证明:(1) ∵ A′B′∥BA,C′B′∥BC, ∴ 四边形ABCB′是平行四边形. ∴ ∠ABC=∠B′(平行四边形的对角相等). 同理∠CAB=∠A′,∠BCA=∠C′. (2) 由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形. ∴ AB=B′C, AB=A′C(平行四边形的对边相等). ∴ B′C=A′C. 同理 B′A=C′A, A′B=C′B. ∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点.  例3(补充)小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由. 解:有6个平行四边形,分别是  ABOF, ABOF, ABCO, ABCO,  BCDO, BCDO, CDEO, CDEO, DEFO, DEFO, EFAO. EFAO.理由是:因为正△ABO≌正△AOF,所以AB=BO,OF=FA.根据 “两组对边分别相等的四边形是平行四边形”,可知四边形ABCD是平行四边形.其它五个同理. |
|
|
第三步:随堂练习 1.如图,在四边形ABCD中,AC、BD相交于点O, (1)若AD=8cm,AB=4cm,那么当BC=___ _cm,CD=___ _cm时,四边形ABCD为平行四边形; (2)若AC=10cm,BD=8cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形. 2.已知:如图,  ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证:EO=OF. ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证:EO=OF.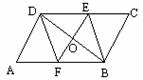 3.灵活运用课本P89例题,如图:由火柴棒拼出的一列图形,第n个图形由(n+1)个等边三角形拼成,通过观察,分析发现: 3.灵活运用课本P89例题,如图:由火柴棒拼出的一列图形,第n个图形由(n+1)个等边三角形拼成,通过观察,分析发现: ①第4个图形中平行四边形的个数为___ __. (6个) ②第8个图形中平行四边形的个数为___ __. (20个) |
|
|
第四步:课后练习: 1、在四边形ABCD中,AC交BD 于点O,若AO=1/2AC,BO=1/2BD,则四边形ABCD是平行四边形.( ) 2、在四边形ABCD中,AC交BD 于点O,若OC= 且 ,则四边形ABCD是平行四边形. 3、下列条件中,能够判断一个四边形是平行四边形的是( ) (A)一组对角相等; (B)对角线相等; (c)一组对角相等; (D)对角线相等; 3、下列条件中能判断四边形是平行四边形的是( ). A、对角线互相垂直 B、对角线相等 C对角线互相垂直且相等 D对角线互相平分 4、已知,如图,平行四边形ABCD的AC和BD相交于O点,经过O点的直线交BC和AD于E、F,求证:四边形BEDF是平行四边形.(用两种方法) 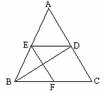 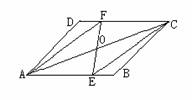 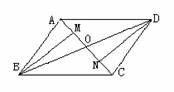 5、已知如图,O为平行四边形ABCD的对角线AC的中点,EF经过点O,且与AB交于E,与CD 交于F.求证:四边形AECF是平行四边形. 5、已知如图,O为平行四边形ABCD的对角线AC的中点,EF经过点O,且与AB交于E,与CD 交于F.求证:四边形AECF是平行四边形. 6、已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN,且BM=DN . 7.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC, 求证:BE=CF |
|
|
课后小结与反思: |
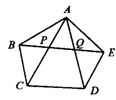
8.已知五边形ABCDE中,AC∥ED,交BE于点P,AD∥BC,交BE于点Q,BE∥CD,求证:△BCP≌△QDE.
7.如图,在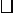 ABCD中,E、F是对角线AC的两个三等分点,求证:四边形BFDE是平行四边形.
ABCD中,E、F是对角线AC的两个三等分点,求证:四边形BFDE是平行四边形.
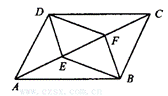
6.已知:在四边形ABCD中,AB∥CD,AB⊥AD,∠AEB=∠CED.F为BC的中点.求证:AF=DF=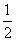 (BF+CE).
(BF+CE).
[聚焦“中考”]
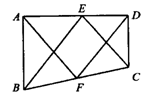
5.已知△ABC中,AD⊥BC于D,E、F、G分别是AB、BD、AC的中点,EG=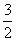 EF,AD+EF=9cm,求△ABC面积.
EF,AD+EF=9cm,求△ABC面积.
4.如图,△ABC中,AD是∠BAC的平分线,CE⊥AD于E,M为BC的中点,AB=14cm,AC=10cm,求ME的长.

[提升“学力”]
3.顺次连结四边形各边中点所得到的四边形是___________.
2.已知△ABC中,D、E分别是AB、AC的中点,F为BC上一点,EF=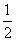 BC,∠EFC=35°,则∠EDF=________.
BC,∠EFC=35°,则∠EDF=________.
第四课时作业优化设计
[驻足“双基”]
1.已知△ABC中,AB:BC:CA=3:2:4且AB=9cm,D、E、F分别是AB、BC、AC的中点,则△DEF的周长是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com