对于上述问题，我们能否运用所学的知识测出旗杆的高度呢？引导学生利用相似三角形的知识来解决问题并展开讨论得出方法.

选一个阳光明媚的日子，请一位的同学量出你在太阳下的影子长度和旗杆影子的长度，再根据你的身高就可以计算出旗杆的高度(如下图).

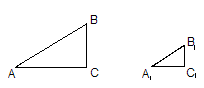
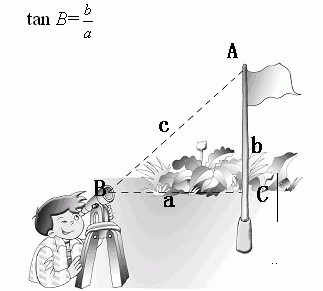
．又因为旗杆和人都垂直于地面，所以∠ACB=∠A₁C₁B₁=90°．所以△ACB∽△A₁C₁B₁．又因为相似三角形对应边成比例，所以有

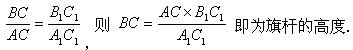
　在上述的问题中，我们利用相似三角形的知识求得了旗杆的高度.

如果没有帮手，又遇上阴天，你能否用其它方法测出旗杆的高度呢？说明你所用方法的依据.

测量在现实生活中随处可见，筑路、修桥等建设活动都离不开测量.当我们走进学校，抬头仰望着旗杆上高高飘扬的五星红旗时，我们也许会想，操场中的旗杆有多高？

6.课外作业与拓展

参见励耘精品系列丛书《课时导航》华师大版八年级(下)P47－P48

5.回顾联系，形成结构

今天我们回顾了测量有关的知识，实际上，我们利用图19.1.2(1)中已知的数据就可以直接计算旗杆的高度，而这一问题的解决将涉及到直角三角形中的边角关系．直角三角形中，三条边有什么关系？它的边与角又有什么关系？这一切都是本章要探究的内容．

4.练习巩固，促进迁移

(1)如图，小明同学拿着一把刻有厘米刻度的小尺，站在距离电线杆约20米的地方，他把手臂向前竖直，小尺伸直，看到尺上约12个刻度恰好遮住电线杆，已知手臂长约为20厘米，你能根据以上数据求出电线杆的高度吗？

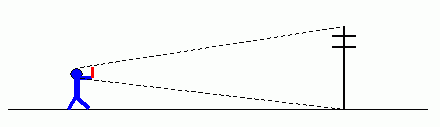
(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P48第9题)

(2)一位同学像利用树影测量树高，他在某一时刻测得长为1米的竹竿影长为0.9米，但当他马上去测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子落在墙上，如图所示，他先测得留在墙上影高为1.2米，又测得地面部分的影长为2.7米，他求得的树高是多少？

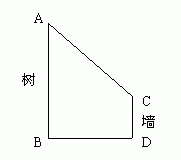
(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P48第10题)

(3)请你与你的同学一起设计两种方案，测量你们学校楼房的高度.(课本例题)

3.巩固应用，拓展研究

为测量某建筑的高度，在离该建筑底部30.0米处，目测其顶，视线与水平线的夹角为40°，目高1.5米．试利用相似三角形的原理，求出该建筑的高度．(精确到0.1米)

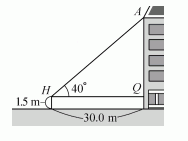
(答案：26.7米)

2.探索交流，形成结构

如图19.1.1，站在操场上，请你的同学量出你在太阳下的影子长度、旗杆的影子长度，再根据你的身高，便可以计算出旗杆的高度．

　　 如果就你一个人，又遇上阴天，那怎么办呢？人们想到了一种可行的方法，还是利用相似三角形的知识．

　　 (回顾前章所学的利用影长测量旗杆的有关知识，同时使学生发现当影长难以找到时，去探究、思考新的方法，激发学生的求知欲及学习兴趣。)

试一试

　　　　 如图19.1.2所示，站在离旗杆BE底部10米处的D点，目测旗杆的顶部，视线AB与水平线的夹角∠BAC为34°，并已知目高AD为1米．现在请你按1∶500的比例将△ABC画在纸上，并记为△A′B′C′，用刻度直尺量出纸上B′C′的长度，便可以算出旗杆的实际高度．

　　　　 你知道计算的方法吗？

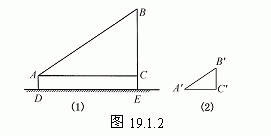
利用△ABC∽△A′B′C′中的对应边成比例可以得到BC的长度。

1.创设情景，导出问题

测量物体的高度是我们在工作和生活中经常遇到的问题.

a²+b²=c²

当你走进学校，仰头望着操场旗杆上高高飘扬的五星红旗时，你也许很想知道，操场旗杆有多高？

你可能会想到利用相似三角形的知识．本章我们将利用直角三角形求解有关的测量的问题。

(通过章前的导图和导入语，指出本章研究的主要内容，使学生在学习之前对本章要学习的内容有所了解，让学生感觉到数学来源于实际生活)

教学重点：用相似三角形的有关知识解决旗杆等物体的测量；

教学难点：培养学数学、用数学的意识与能力。

2.经历由实际情景引出问题，探索掌握有关的数学知识内容，再运用于实践的过程，培养学数学、用数学的意识与能力。