3、观察发现，命题结构。

观察下列命题，你能发现这些命题有什么共同的结构特征？与同样交流。

(1)如果两个三角形的三条边相等，那么这两个三角形全等；

(2)如果一个三角形是等腰三角形，那么这个三角形的两个底角相等；

(3)如果一个四边形的对角线相等，那么这个四边形是矩形；

(4)如果一个四边形的一组对边平行且相等，那么这个四边形是平行四边形；

(5)如果一个四边形的两条对角线互相垂直，那么这个四边形是菱形。

总结：在数学中，许多命题是由题设(或条件)和结论两部分组成的．题设是已知事项，结论是由已知事项推出的事项．这种命题常可写成“如果……那么……”的形式．其中，用“如果”开始的部分是题设，用“那么”开始的部分是结论．例如，在命题(1)中，“两个角是对顶角”是题设，“这两个角相等”是结论。

例、把命题“在一个三角形中，等角对等边”改写成“如果……那么……”的形式，并分别指出命题的题设与结论．

　　解：这个命题可以写成：“如果在一个三角形中有两个角相等，那么这两个角所对的边也相等.” 这里的题设是“在一个三角形中有两个角相等”，结论是“这两个角所对的边也相等”。

练习：课本P3　 练习2

2、思考：得出命题

思考：试判断下列句子是否正确。

(1)如果两个角是对顶角，那么这两个角相等；

(2)三角形的内角和是180°；

(3)同位角相等；

(4)平行四边形的对角线相等；

(5)菱形的对角线相互垂直

根据已有的知识可以判断出句子(1)、(2)、(5)是正确的，句子(3)、(4)是错误的．像这样可以判断它是正确的或是错误的句子叫做命题(proposition)．正确的命题称为真命题，错误的命题称为假命题。

练习：

(1)下列句子哪些是命题？

①动物都需要水；

②猴子是动物的一种；

③玫瑰花是动物；

④美丽的天空；

⑤对应角都相等的两个三角形一定全等；

⑥负数都小于零；

⑦你的作业做完了吗？

⑧所有的质数都是奇数；

⑨过直线外一点作l的平行线；

⑩如果，，那么。

(2)练习：课本P3　 练习1

1、试一试：得出定义

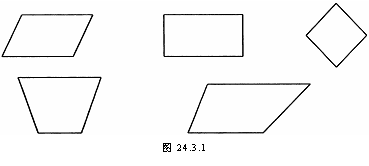
你是如何找出图中的平行四边形呢？

“有两组对边分别平行的四边形叫做平行四边形”这句话说明了平行四边形的含义以及区别于其他图

形的特征。

一般地，能明确指出概念含义或特征的句子，称为定义。

例如：(1) 有一个角是直角的三角形，叫做直角三角形．

(2) 有六条边的多边形，叫做六边形．

(3)　 在同一平面内，两条不相交的直线叫做平行线．

你还能举出一些其他的例子吗？

观察这些定义，你发现定义中用词有什么特征？

同学们各抒己见后，总结：定义必须是严密的．一般避免使用含糊不清的术语，比如“一些”、“大概”、

“差不多”等不能在定义中出现．正确的定义能把被定义的事物或名词与其他的事物或名词区别开来。

19.1．1　 命题与定理 第一课时 命题 教学目标 1、知识与技能：了解命题、定义的含义；对命题的概念有正确的理解。会区分命题的条件和结论。知道判断一个命题是假命题的方法。 2、过程与方法： 结合实例让学生意识到证明的必要性，培养学生说理有据，有条理地表达自己想法的良好意识。 3、情感、态度与价值观：　 初步感受公理化方法对数学发展和人类文明的价值。 重点与难点 1、重点： 找出命题的条件(题设)和结论。 2、难点： 命题概念的理解。 教学过程 一、复习引入 　　 教师：我们已经学过一些图形的特性，如“三角形的内角和等于180度”，“等腰三角形两底角相等”等。根据我们已学过的图形特性，试判断下列句子是否正确。 1、如果两个角是对顶角，那么这两个角相等； 2、两直线平行，同位角相等； 3、同旁内角相等，两直线平行； 4、平行四边形的对角线相等； 5、直角都相等。 二、探究新知 (一)命题、真命题与假命题 　　　 学生回答后，教师给出答案：根据已有的知识可以判断出句子1、2、5是正确的，句子3、4水错误的。像这样可以判断出它是正确的还是错误的句子叫做命题，正确的命题称为真命题，错误的命题称为假命题。 　　　 教师：在数学中，许多命题是由题设(或已知条件)、结论两部分组成的。题设是已知事项；结论是由已知事项推出的事项，这样的命题常可写成“如果.......，那么.......”的形式。用“如果”开始的部分就是题设，而用“那么”开始的部分就是结论。例如，在命题1中，“两个角是对顶角”是题设，“这两个角相等”就是结论。 　　　 有的命题的题设与结论不十分明显，可以将它写成“如果.........，那么...........”的形式，就可以分清它的题设和结论了。例如，命题5可写成“如果两个角是直角，那么这两个角相等。” (二)实例讲解 　　 1、教师提出问题1(例1)：把命题“三个角都相等的三角形是等边三角形”改写成“如果.......，那么.......”的形式，并分别指出命题的题设和结论。 学生回答后，教师总结：这个命题可以写成“如果一个三角形的三个角都相等，那么这个三角形是等边三角形”。这个命题的题设是“一个三角形的三个角都相等”，结论是“这个三角形是等边三角形”。 　　 2、教师提出问题2：把下列命题写成“如果.....，那么......”的形式，并说出它们的条件和结论，再判断它是真命题，还是假命题。 (1)对顶角相等； (2)如果a＞ b,b＞ c, 那么a=c； (3)菱形的四条边都相等； (4)全等三角形的面积相等。 　 学生小组交流后回答，学生回答后，教师给出答案。 (1)条件：如果两个角是对顶角；结论：那么这两个角相等，这是真命题。 (2)条件：如果a＞ b,b＞ c；结论：那么a=c；这是假命题。 (3)条件：如果一个四边形是菱形；结论：那么这个四边形的四条边相等。这是真命题。 (4)条件：如果两个三角形全等；结论：那么它们的面积相等，这是真命题。 (三)假命题的证明 　　　 教师讲解：要判断一个命题是真命题，可以用逻辑推理的方法加以论证；而要判断一个命题是假命题，只要举出一个例子，说明该命题不成立，即只要举出一个符合该命题题设而不符合该命题结论的例子就可以了，在数学中，这种方法称为“举反例”。 　　　 例如，要证明命题“一个锐角与一个钝角的和等于一个平角”是假命题，只要举出一个反例：60度角是锐角，100度角是钝角，但它们的和不是180度即可。 三、随堂练习 　　 课本P65练习第1、2题。 四、总结 1、什么叫命题？什么叫真命题？什么叫假命题？ 2、命题都可以写成“如果.....，那么.......”的形式。 3、要判断一个命题是假命题，只要举出一个反例就行了。 五、布置作业 　　 　课本习题19.1第1题、第2题。 六、板书设计 　　　 黑板分为左、中、右三部分，中间与右边用于教师板书例题等，左边用于板书以下内容： 1、可以判断它是正确的或是错误的句子叫做命题； 　　 正确的命题叫真命题，错误的命题叫假命题。 2、命题都可以写成“如果.......，那么........”的形式。 3、要判断一个命题是假命题，只要举出一个反例就可以了。

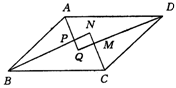
　　 如图所示，ABCD中，AQ，BN，CN，DQ分别是∠DAB，∠ABC，∠BCD，∠CDA的平分线，AQ与BN交于P，CN与DQ交于M，在不添加其他条件的情况下，试写出一个由上述条件推出的结论，并给出证明过程．(推理过程中用到平行四边形和角平分线这两个条件)

在四边形ABCD中，给出下列论断：①AB∥DC；②AD=BC；③∠A=∠C．以其中两个作为条件，另外一个作为结论，用“如果……那么……”的形式，写出一个你认为正确的命题．

6．在一次数学竞赛中，A，B，C，D，E五位同学分别得到了前五名(没有并列同一名次的)．关于各人的名次大家作出了下面的猜测：

　　 A说：“第二名是D，第三名是B”．　　 B说：“第二名是C，第四名是E．”

　　 C说：“第一名是E，第五名是A．”　　 D说：“第三名是C，第四名是A．”

　　 E说：“第二名是B，第五名是D．”

结果每人都只猜对了一半，请判断他们的名次如何．

5．证明：两条平行线被第三条直线所截，则它们的一对同位角的平分线互相平行．(要求画图，写出已知、求证、证明)

4．某工程队，在修建兰定高速公路时，有时需将弯曲的道路改直，根据什么公理可以说明这样做能缩短路程(　 )

　　 A．直线的公理;　　 　B．直线的公理或线段最短公理

　　 C．线段最短公理;　　 D．平行公理