
 (一)、填空题:
(一)、填空题:
1、有一边对应相等的两个 三角形全等;
2、有一边和 对应相等的两个三角形全等;
3、有两边和 一角对应相等的两个三角形全等;
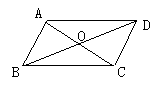
4、如图,AB∥CD,AD∥BC,AC、BD相交于点O.
(1)由AD∥BC,可得 =
= ,由AB∥CD,可得
,由AB∥CD,可得 =
= ,又由 ,于是△ABD≌△CDB;
,又由 ,于是△ABD≌△CDB;
(2)由 ,可得AD=CB,由 ,可得△AOD≌△COB;
(3)图中全等三角形共有 对.
1、如图,在△ABC中,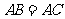 ,
,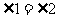 ,试说明△AED是等腰三角形.
,试说明△AED是等腰三角形.
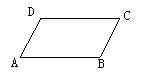 2、如图,AB∥CD,AD∥BC,
2、如图,AB∥CD,AD∥BC,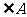 与
与 ,
,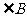 与
与 相等吗?说明理由.
相等吗?说明理由.
3、范例
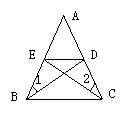
例:如图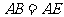 ,
,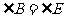 ,
,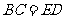 ,点F是CD的中点,
,点F是CD的中点,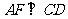 吗?试说明理由.
吗?试说明理由.
教学要点:
(1)分析题目结论假定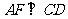 ,可转化为
,可转化为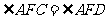 ,需证它们所在的两个三角形全等;
,需证它们所在的两个三角形全等;
(2)观察图形,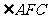 、
、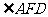 中,并不在三角形中,为此添辅助线AC、AD;
中,并不在三角形中,为此添辅助线AC、AD;
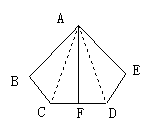 (3)在△ACF与△ADF中,已知AF是公共边,CF=FD,尚缺一条件,它只能是AC与AD相等;
(3)在△ACF与△ADF中,已知AF是公共边,CF=FD,尚缺一条件,它只能是AC与AD相等;
(4)为证AC与AD相等.又要找它们分别在的△ACB与△ADE;
(5)△ACB与△ADE,由已知条件可由SAS证它们全等;
(6)书写范例.
解:连结AC、AD,由已知AB=AE,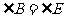 ,BC=DE
,BC=DE
由SAS三角形全等判定法可知:
△ABC≌△AED
根据全等三角形的对应相等可知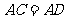
 由
由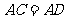 ,
,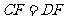 ,
,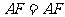 (公共边),
(公共边),
根据SSS可知△ACF≌△ADF
根据全等三角形的对应角相等可知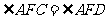
又由于F在直线CD上,可得 ,即
,即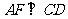 .
.
你们可有其他方法吗?
2、填下表(挂出小黑板,让学生思考、讨论,共同填答).
|
两个三角形中对应相等的元素 |
两个三角形是否全等 |
依据的判定法 |
反例 |
|
SSS |
√ |
SSS |
|
|
SAS |
√ |
SAS |
|
|
SSA |
X |
可举反例 |
 |
|
ASA |
√ |
ASA |
|
|
AAS |
√ |
AAS |
 |
|
AAA |
X |
可举反例 |
 |
1、演示
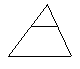
(1)演示图1中的I、II三角形,它们间有两边及一对角对应相等,这两个三角形能完全重合,是全等形.但再取出III的三角形与I叠在一起后,发现它们不重合不是全等形,因此我们进一点证实了:有两边和其中一边的对角对应相等的两个三角形不一定全等.“SSA”不是判定三角形全等的方法.
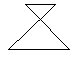
(2)演示图2中的I、II三角形,它们间有三个角对应相等,这两个三角形能完全重合,是全等形,但再取出III的三角形与I叠在一起后,发现它们不重合,不是全等形.因此我们进一步证实了:三个角对应相等的两个三角形不一定全等“AAA”也不是判定三角形全等的方法.
2、一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种判定法,还有其他的三角形全等判定法吗?比如说“SSA”、“AAA”能成为判定两个三角形全等的条件吗?
1、判定两个三角形全等的条件有哪些?
(有SAS、ASA、AAS、SSS.HL)
(三)教学过程
[复习引入]
什么样的二次根式叫做最简二次根式?(由学生回答)
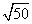 与
与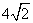 的形式与实质是什么?
的形式与实质是什么?
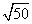 可以化简为
可以化简为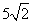 .继续提问:
.继续提问: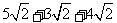 ,可以化简吗?
,可以化简吗?
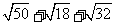 ,可以化简吗?
,可以化简吗?
这就是本节课研究的内容--二次根式的加减法.
[讲解新课]
问题:已知△ABC中,如果∠C=90°,AB=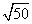 m,BC=
m,BC=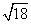 m,那么△ABC的周长L等于多少呢?
m,那么△ABC的周长L等于多少呢?
 分析:要想知道周长L,必须先求出AC长度,因为△ABC为Rt △,所以可由勾股定理求得AC。
分析:要想知道周长L,必须先求出AC长度,因为△ABC为Rt △,所以可由勾股定理求得AC。
解:∵在△ABC中,∠C=90°,∴利用勾股定理,可得:
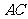
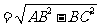
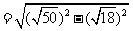
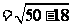
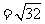 (m)
(m)
故周长L=AB+BC+AC=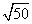 +
+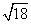 +
+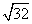 (m)
(m)
那么,在此就要解决我们上面提出的问题: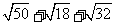 是最后结果吗?可以化简吗?我们知道
是最后结果吗?可以化简吗?我们知道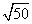 ,
,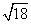 ,
,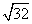 都不是最简二次根式,下面把这几个数来化简,看看形式上有什么共同特征:
都不是最简二次根式,下面把这几个数来化简,看看形式上有什么共同特征: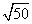
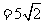 ,
,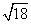
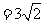 ,
,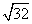
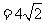 。我们发现这几个二次根式化成最简二次根式以后,它们的被开方数完全相同,那么象这样的几个二次根式就叫做同类二次根式。于是周长L=AB+BC+AC=
。我们发现这几个二次根式化成最简二次根式以后,它们的被开方数完全相同,那么象这样的几个二次根式就叫做同类二次根式。于是周长L=AB+BC+AC=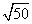 +
+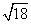 +
+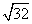 =
=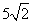 +
+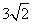 +
+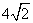 =
=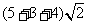 =
=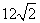 (m)
(m)
定义:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
类比、迁移、感悟:合并同类二次根式可以类似于合并同类项法则进行。(通过一段视频让学生了解。)
二次根式加减法的一般思路:
(1)如果几个二次根式被开方数相同,那么可以直接根据分配律进行加减运算;
(2)如果所给二次根式不是最简二次根式,应该先化简,再考虑进行加减运算.
例题分析
例1 下列各式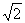 ,
,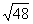 ,
,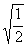 ,
,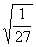 ,
,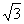 ,
,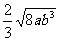 ,
,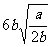 中,哪些是同类二次根式?
中,哪些是同类二次根式?
解:∵
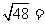
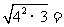
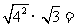
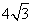 ,
,
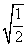
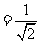
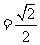 ,
,
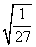
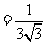
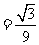
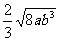
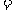
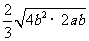
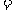
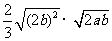
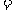
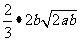
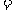
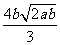
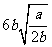
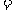
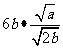
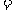
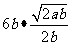
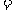
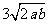
∴
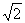 ,
,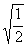 是同类二次根式,
是同类二次根式,
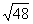 ,
,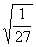 ,
,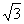 是同类二次根式,
是同类二次根式,
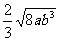 ,
,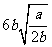 是同类二次根式,
是同类二次根式,
小结:要想了解几个二次根式是否为同类二次根式,必须先化成最简二次根式,再看被开方数相同是否相同,与最简二次根式前面的因式及符号无关.
课堂练习一:
1.在下列各组根式中,是同类二次根式的是( )
(A)
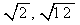 (B)
(B)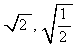 (C)
(C)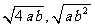 (D)
(D)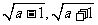
2.下列各式中与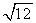 是同类二次根式的是( )
是同类二次根式的是( )
(A)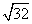 (B)
(B)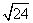 (C)
(C)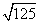 (D)
(D)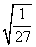
3.判断:下列计算是否正确?为什么?
 ;
;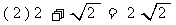
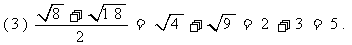
说明:不是同类二次根式不能合并(如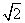 与
与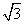 )。
)。
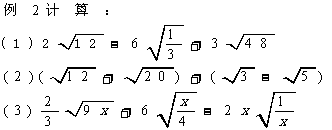
分析:先化简,再寻找,最后合并。
解: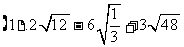
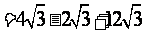
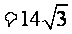 ;
;
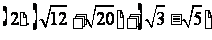
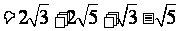
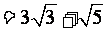 ;
;
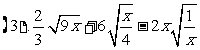
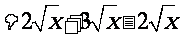
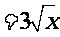 。
。
小结:
(1)如果几个二次根式的被开方数相同,那么可以直接根据分配律进行加减运算.
(2)如果所给的二次根式不是最简二次根式,应该先把各个二次根式化成最简二次根式,再根据分配律进行加减运算.
(3)合并方法为系数相加减,根式不变,不是同类二次根式的不能合并。合并同类二次根式与合并同类项类似,因此,二次根式的加减可以对比整式的加减进行。
课堂练习二:
1.计算:
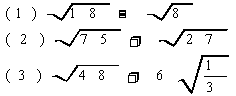
2.选择:下列计算正确的是( )
(A)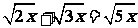 (B)
(B) 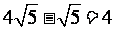
(C)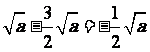 (D)
(D)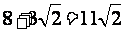
交流、归纳:二次根式加减法的步骤:
(1) 将每个二次根式化为最简二次根式;
(2) 找出其中的同类二次根式;
(3) 合并同类二次根式。
简单地说:一化,二找,三合并。
3、计算:(1)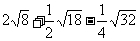 . (2)
. (2)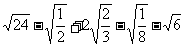
(二)整体感知
同类二次根式的概念应分二层含义去理解(1)化简后(2)被开方数还相同.通过正确理解二次根式加减法的法则来准确地实施二次根式加减法的运算,应特别注意合并同类二次根式时仅将它们的系数相加减,根式一定要保持不变,并可对比整式的加减法则以增加对合并同类二次根式的理解,增强综合运算的能力.
(-)明确目标
学习二次根式化简的目的是为了能将一些最终能化为同类二次根式项相合并,从而达到化繁为简的目的,本节课就是研究二次根式的加减法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com