3．合作探究

　　 (1)整体感知

　　 通过课前复习和热身，整体感知这节课的目标和两个三角形有“两角和一边”分别对应相等的两种情形以及这两种情形的统一；随之探索两个三角形全等的识别方法──(ASA)或(AAS)．

　　 (2)四边互动

　　 互动1

　　 师：在课前热身的问题(2)中，已知“角边角”与“角角边”这两种情形可以互相转化吗？为什么？

　　 生：可以，由三角形的内角和等于180°可知．

　　 明确　 由三角形的内角和等于180°可知：已知两个三角形有“两角和它们的夹边”与“两角和其中一角的对边”对应相等，这两种情形是完全一样的．

　　 互动2

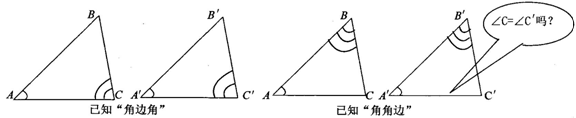
　　 师：请完成教材第87页的“做一做”，将你们的结果互相交流一下，是否全等？

　　 明确　 如果两个三角形有两角及其夹边分别对应相等，那么这两个三角形全等[简记为(ASA)]．

　　 互动3

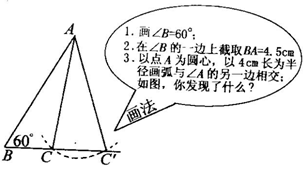
　　 师：如果将课本的“做一做”加以改变：以这两个角为内角，以这条线段为40°的对边，画一个三角形．该怎样画呢？

生：画图(可能有些棘手，师点拨──点拨①：这是个“角角边”条件，它能转化为“角边角”吗？点拨②：如何将其转化为“角边角”呢)最后得出结论：可以采用如图的做法，利用三角形的内角和等于180°，先画出第三个变相已知的内角──80°，从而将问题成功地转化为“已知：两角分别为60°、80°和它们的夹边为4．5cm，画这个三角形．”

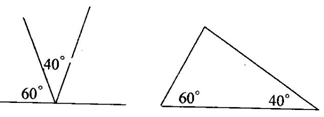
　　 师：刚才的画图结果，说明了什么？

　　 生：已知两角及其中一角的对边时，这两个三角形全等．

　　 明确　 如果两个三角形有两个角及其中一角的对边对应相等，那么这两个三角形全等[简记为(AAS)]．

　　 互动4

　　 师：通过以上探索，我们能否得出结论：如果两个三角形的两角和一边对应相等，那么这两个三角形全等吗？

　 　明确 　如果两个三角形有两个角及一边对应相等，那么这两个三角形全等[简记为(ASA)或(AAS)]．

2．课前热身

　　 (1)如果已知两个三角形有两角和一边对应相等，应分几种情形讨论？

(2)先仔细观察，看一看如图所示的①、②两图中的已知条件可以转化为一样的吗？为什么？

1．复习导入

　　 两个三角形已知三个部分对应相等时，除了三边、三角、两边和一角外，还有什么？

　　 讨论已知“两角和一边”的情形；并通过画图的方式探索两个三角形全等的识别方法之(ASA)．

2．实践探索

(1)实践活动：小明不小心打翻了墨水，将自己所画的三角形涂黑了，如图24-2-14所示，你能帮小明想想办法，画一个与原来的三角形完全一样的三角形吗？

　　 (2)巩固练习

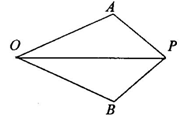
①如图所示，已知OP平分∠AOB，OA=OB，那么△AOP≌△BOP，为什么？

②如图所示，已知的相等条件已在图中标出，要使这两个三角形全等，还需要增加一个什么条件？你有哪几种增加方法？

③如图所示，已知AD=BC，∠ADC=∠BCD，那么∠BDC=∠ACD吗？为什么？

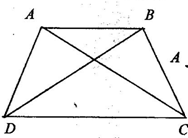
④如图所示，已知AE=DB，BC=EF，BC∥EF，说明△ABC和△DEF全等的理由．

[答案]　 ①SAS　 ②∠C=∠E或AB=FD　 ③相等，∵△ADC≌△BCD(SAS)　 

④AB=ED，BC=EF，∠FED=∠ABC，∴△ABC≌△EDF(SAS)

1．链接生活

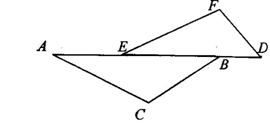
如图所示，要测量一个不能直接测量的池塘的宽AB，有位同学是这样做的：先在平地上选择一个可以同时到达A、B两点的点C；然后分别连接AC并延长到D，使DC=AC，连接BC并延长到点E，使EC=BC；这时他就断定线段DE的长就是池塘AB的宽．你认为这位同学的说法正确吗？为什么？

5．学习小结

　　 (1)内容总结

　　 ①探索两个三角形全等的识别方法──(SAS)．

　　 ②方法归纳：在探索全等三角形的识别方法的时候，都用实际操作──画图来说明和解决问题的，这是一种常见的、有效的、颇具说服力的方法．正所谓：实践是检验真理的惟一标准．

4．达标反馈

(1)如图所示，△ABC中，AB=AC，平分∠BAC，试说明△ABD≌△ACD．

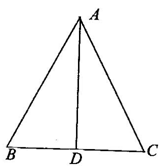
　　 [答案]　 ∵AB=AC，AD平分∠BAD，∴∠BAD=∠CAD，∴△ABD≌△ACD(SAS)

(2)根据图所标注的条件，判断下面的两个三角形是否全等？

　　 [答案]　 全等

(3)如图所示，点M是等腰梯形ABCD的底边AB的中点，△AMD≌△BMC吗？试说明理由．

　　 [答案]　 ∵M为AB中点，AD=BC，∴AM=BM，∠A=∠B，∴△AMD≌△BMC(SAS)

3．合作探究

　　 (1)整体感知

　　 通过课前复习和热身，整体感知我们这节课的目标以及两个三角形有三个内角对应相等，不能识别它们全等；并为这节课的主要目标──“已知两边和一角”的识别方法的探索打开话匣子．

　　 (2)四边互动

　　 互动1

　　 师：在刚才的问题中，我拿的大三角板与你的相应的小三角板只存在什么关系？这说明了什么？

　　 生：相似但不一定全等；这说明如果两个三角形有三个角对应相等，它们不一定全等．

　　 师：如果已知两个三角形有两边和一角对应相等，应分几种情形呢？

　　 师：(讨论、交流)两种；两边和它们的夹角，两边和其中一边的对角．(学生的语言可能不到位，师可通过图形让学生具体地说出边、角，师再将其归纳成以上两类)

　　 明确　 已知三角的不可识别以及已知两边和一角的分类结果．

　　 互动2

　　 师：下面请同学们完成第85页的“做一做”，完成以后，互相交流一下，看是否全等？

　　 明确　 如果两个三角形有两边及其夹角分别对应相等，那么这两个三角形全等．[简记为(SAS)]

　　 互动3

师：同学们再来画一画第86页的“做一做”，看看结果如何？

　　 师：刚才的画图结果(如图所示)，说明了什么？

　　 生：已知两边及其中一边的对角时，画出的三角形可能有两种，因此它们不一定全等．

　　 师：想想看，何时其图形只有一种呢？

　　 生：(可能答不上来，师点拨并结合图形说明：点拨①，当AC的长度恰好是点A到BC的距离，即AC⊥BC；点拨②，当AC≥AB．画图的结果如何？)

　 　明确　 (SSA)不能作为识别两个三角形全等的方法的依据．