4．达标反馈

　　 (1)填空：请用类比思想猜想一下：全等三角形可能还有哪些识别方法？试写出一两个填在题后的横线上：　 SAS，ASA　 ．(注：可用简记的形式．角相等可用其英文“angle”的首大写字母“A”来表示)

(2)如图1所示，四边形ABCD中，AD=BC，AB=DC，△ABC≌△CDA吗？试说明理由．

　　　　　 (1)　　　　　　　　　　　　　　　 (2)

　　 [答案]　 全等；满足SSS这个条件．

　　 (3)根据图2所标注的条件，判断三角形是否全等？

　　 [答案]　 全等

3．合作探究

　　 (1)整体感知

　　 整体感知两个三角形全等的识别条件至少要有三个相等的部分，然后通过画图操作，验证这一感知，最后通过分类讨论、画图操作得出全等三角形的识别方法之一──(SSS)．

　　 (2)四边互动

　　 互动1

　　 师：刚才的一位同学已经回答了：两个三角形全等的识别条件至少要有三个相等的部分．可能有的同学对此将信将疑，下面我们从最简单的开始分类讨论一下：如果只知道两个三角形有一个部分对应相等，那么这个相等的部分是什么，有哪几种可能？

　　 明确 　感知分类的方法及明确只有一个相等的部分，两个三角形一定不全等．

　　 互动2

　　 师：如果两个三角形有两个相等的部分，那么有几种可能的情形呢？

　　 生：三种；两个三角形有：两条边对应相等、两个角对应相等、一边一角对应相等．

　　 师：画画看，它们全等吗？

　　 生：(画图交流之后)……)不全等．

　　 明确 　两个三角形有两个部分对应相等，它们也不全等．

　　 互动3

　　 师：如果两个三角形有三个部分分别对应相等，想一想：有哪几种可能的情形？

　　 生：(交流并讨论……)有四种情形：(1)三条边对应相等；(2)三个角对应相等；(3)两边和一角对应相等；(4)两角和一边对应相等．

　　 明确 　了解分类的方法与思想；明确两个三角形有三个部分对应相等，应分成四种不同的情形．

　　 互动4

　　 师：下面我们就以上四种情形分别进行讨论，首先我们讨论第一种情形：已知两个三角形有三条边对应相等．同学们把书翻到第83页，操作一下83页的“做一做”，分四个小组进行操作：每小组所给的三条线段分别是：第①小组：a=4cm、b=3cm、c=4.8cm；第②小组：a=2cm、b=3cm、c=4cm；第③小组：a=4cm、b=5cm、c=6cm；第④小组：a=3cm、b=3cm、c=5cm．

　　 生：学生分组画三角形(大约5分钟)．

　　 师：怎样检验你们每小组所画的三角形全等？它们全等吗？这说明了什么？

　　 生：将其对应顶点叠在一起，看是否重合；它们确实是全等的；这说明两个三角形若有三条边对应相等，这两个三角形是全等的．

　　 师：板书结论：如果两个三角形的三条边分别对应相等，那么这两个三角形全等[简记为(SSS)]．

　　 明确　 如果两个三角形的三条边分别对应相等，那么这两个三角形全等[简记为(SSS)]．

2．课前热身

　　 我们已经知道：全等三角形的识别方法有SAS,ASA(AAS)，你认为两个三角形全等的识别条件至少要有几个？

1．复习导入

　　 (1)若两个三角形的三条边、三个内角分别对应相等，这两个三角形全等吗？

　　 (2)全等三角形有哪些识别方法？

　　 通过复习全等三角形的识别方法，探索全等三角形的识别条件的个数及全等三角形的识别方法之一──(SSS)

2．实践探索

　　 (1)实践活动

小明不小心将一块三角形的玻璃打碎成三小块，如图所示，现准备到玻璃店配一块完全一样的三角形玻璃，你认为带哪一小块去合适？为什么？

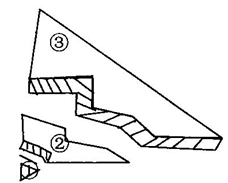
　　 (2)巩固练习

①如图所示，AD=BE，AC∥DF，BC∥EF，△ABC≌△DEF吗？为什么？

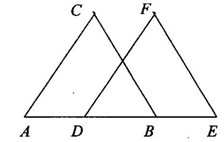
　　 [答案]　 全等(ASA)

②如图所示，已知的相等条件已在图中标出，要使这两个三角形全等，还需要增加一个什么条件？你有哪几种增加方法？

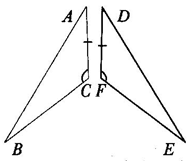
　　 [答案]　 BC=EF(SAS)，∠B=∠E(AAS)，∠A=∠D(ASA)

③如图所示，已知：∠BDA=∠CEA，AE=AD，说明AB=AC的理由．

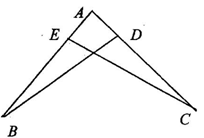
　　 [答案]　 ∵△ABD≌△ACE，∴AB=AC

④如图所示，已知：∠C=∠D，CE=DE，那么∠DAB=∠ABC吗？为什么？

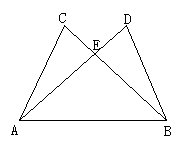
　　 [答案]　 相等，因为△ABD≌△BAC

1．链接生活

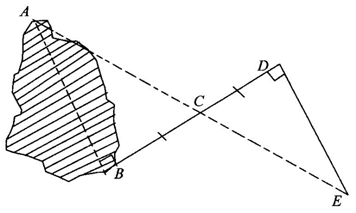
如图所示，要测量一个不能直接测量的池塘的宽AB，有位同学是这样做的：先过B点画直线AB的垂线BC，延长BC到D，使DC=BC；然后画BD的垂线并在其垂线上选择一点E，使E、C、A三点在同一条直线上，连接DE；这时他就断定线段DE的长就是池塘AB的宽．你认为这位同学的说法正确吗？为什么？

5．学习小结

　　 (1)内容总结

　　 ①探索两个三角形全等的识别方法──(ASA)或(AAS)；

　　 ②这两种方法的统一：如果两个三角形有两个角及一边对应相等，那么这两个三角形全等．

　　 (2)方法归纳：已知“两角和其中一角的对边”，画这个三角形时，我们所采用的处理问题的方法仍然是前面已学习过的转化思想．化未知“角角边”为已知的“角边角”，从而使问题迎刃而解．

4．达标反馈

(1)如图所示，∠ABC=∠DCB，∠ACB=∠DBC，试说明△ABC≌△DCB吗？

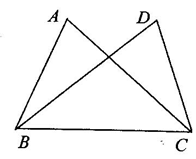
　　 [答案]　 全等(ASA)

(2)根据图所标注的条件，判断下面的三角形是否全等？并说明理由．

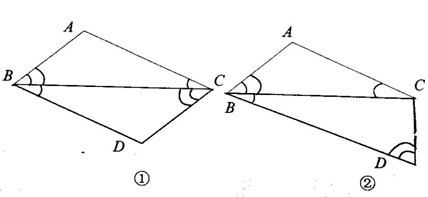
　　 [答案]　 ①能，△ABC≌△DCB(ASA)　 ②不能

(3)如图所示，△ABC是等腰三角形，BD、CE分别是∠B、∠C的平分线，△BEC≌△CDB吗？试说明理由．

　　 [答案]　 全等(ASA)