5．学习小结

　　 (1)内容总结

　　 ①探索两个直角三角形全等的识别方法中的条件的个数：(除直角相等外)只需两个(其中至少有一个条件是边相等)；

　　 ②两个直角三角形全等的识别方法，特别(HL)的识别方法．

　　 (2)方法归纳：在本节课的探索直角三角形全等的条件的个数的过程中，我们仍然采用了“从特殊到一般”的数学方法，在一般三角形全等的识别方法的基础上，探索出两个直角三角形全等的条件．

4．达标反馈

⑴如图所示，AC=AD，∠C=∠D=90°，试说明BC=BD的理由．

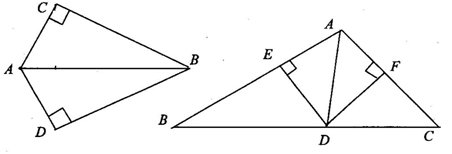
　　 [答案]　 ∵AC=AD，∠C=∠D，∠ABC=∠ABD，∴△ABC≌△ABD(HL)，∴BC=BD

　　 ⑵如上右图所示，AD是∠BAC的平分线，DE⊥AB于E、DF⊥AC于F，试说明AE=AF的理由．

[答案]　 ∴∠AED=∠AFD=90°，DE=DF，∠BAD=∠CAD，

∴△ADE≌△ADF(HL)，∴AE=AF

3．合作探究

　　 (1)整体感知

　　 通过课前复习和热身，整体感知这节课的目标和两个直角三角形全等的识别方法中的条件的个数，并为本节课的中心话题──(HL)这一问题的提出埋下伏笔．

　　 (2)四边互动

　　 互动1

　　 师：在课前热身的问题(2)中，除两个直角对应相等外，若再增加一边一角分别对应相等，这两个直角三角形为什么全等？

　　 生：因为无论增加哪一边或哪一角，再加上两个直角对应相等，都符合两个三角形全等的识别方法(ASA)或(AAS)．

　　 明确　 已知一锐角和一边分别对应相等的两个直角三角形全等．

　　 互动2

　　 师：若增加的条件是两条边分别对应相等吗？

　 　生：不一定；若增加的两条边是两条直角边，则由(SAS)可判断它们全等；若增加的条件是一直角边和斜边分别对应相等，这是已知(SSA)则不一定全等．(可能有些同学会说全等，师应鼓励)

师：回答得很全面，但果真如此吗？如图24-2-30所示，让我们来回想一下前面所学的“已知两个三角形有两边和其中一边的对角分别对应相等”的画图，当AC⊥BC时，这样的三角形可画几个呢？

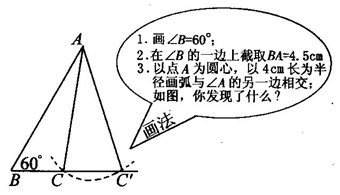
　　 生：一个．

　　 师：由此你有什么感悟？

　　 生：在直角三角形中，已知(SSA)能识别这两个直角三角形全等．

　　 师：猜测终究是猜测，让我们先来完成第89页的“做一做”后，再下结论．

　　 明确　 判断两个直角三角形全等的条件(除直角相等外)只需两个(其中至少有一个条件是边相等)；重点明确(HL)的识别方法．

2．课前热身

如图所示：(1)在Rt△ABC与Rt△A′B′C′中，已经知道哪两个角相等？

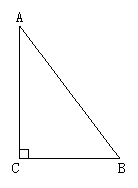
　　 (2)若除∠C=∠C′外，另增加相等条件：①一边一角分别对应相等；②两边分别对应相等；这两个直角三角形全等吗？为什么？

1．复习导入

　　 两个三角形全等的识别方法有哪些？

　　 探索直角三角形全等的识别方法．

2．实践探索

　　 (1)实践活动

如图所示，四边形ABCD是平行四边形，△ABC与△CDA是否全等？若四边形是菱形、矩形、正方形、梯形，是否有相同的结论？

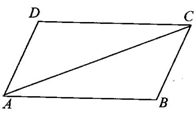
　　 (2)巩固练习

①如图所示，四边形ABCD是平行四边形，你能用今天所学的知识说明∠B=∠D吗？

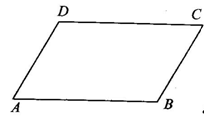
　　 [答案]　 能，连接AD，则△ABD≌△DCA，所以∠B=∠C．

②如图所示，已知AC=BD，AD=BC，那么∠C=∠D吗？为什么？

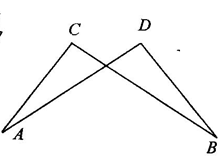
　　 [答案]　 能，因为由SSS知△ABD≌△BAC

③如图所示，已知AB=AC，AD=AE，BD=CE，△ABE≌△ACD吗？说明理由．

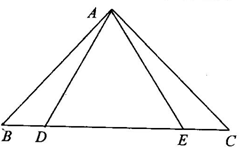
　　 [答案]　 全等，因为满足SSS这个条件．

1．链接生活

如图所示，木匠师傅在做门、窗时，常在做好的门窗上加一根斜木条，你知道这是为什么吗？

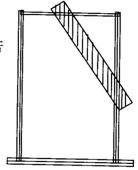
5．学习小结

　　 (1)内容总结

　　 ①探求两个三角形全等的识别方法的条件的个数；

　　 ②全等三角形的识别方法之(SSS)；

　　 (2)方法归纳：在本节课教学时，我们在探索三角形全等的识别方法的条件的个数，用到了我们在前面已提到过的分类思想；并且在得出(SSS)这一识别方法时，我们把它与两个相似三角形的识别方法予以比较，不仅让同学们进一步感受到全等三角形是相似三角形的相似比为1时的特例，而且用类比的方法让同学们隐隐约约地感悟：全等三角形的其他识别方法的存在，为我们下节课的教学作了一个很好的铺垫．