
3. 如图,如果要使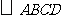 成为一个菱形,
成为一个菱形,
需要添加一个条件,那么你添加的条件是 .
2. 如图,在菱形ABCD中,不一定成立的( )
如图,在菱形ABCD中,不一定成立的( )
A.四边形ABCD是平行四边形
B.AC⊥BD
C.△ABD是等边三角形
D.∠CAB=∠CAD
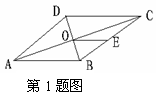
1. 如图,在菱形ABCD中,对角线AC、BD相交于点O,E为BC的
中点,则下列式子中一定成立的是( )
 A.AC=2OE
B.BC=2OE
A.AC=2OE
B.BC=2OE
C.AD=OE D.OB=OE
10. (1)证明:∵MN∥BC,∴∠BCE=∠CEO又∵∠BCE=∠ECO
∴∠OEC=∠OCE,∴OE=OC,同理OC=OF,∴OE=OF
(2)当O为AC中点时,AECF为矩形,∵EO=OF(已证),OA=OC
∴AECF为平行四边形,又∵CE、CF为△ABC内外角的平分线
∴∠EOF=90°,∴四边形AECF为矩形
 课时二菱形
课时二菱形
9. 猜想结果:图2结论S△PBC=S△PAC+S△PCD; 图3结论S△PBC=S△PAC-S△PCD
证明:如图2,过点P作EF垂直AD,分别交AD、BC于E、F两点.
∵ S△PBC=BC·PF=BC·PE+BC·EF
=AD·PE+BC·EF=S△PAD+S矩形ABCD
S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD
∴ S△PBC=S△PAC+S△PCD
8. 连接AC、BD,AC与BD相交于点O,连接OE
连接AC、BD,AC与BD相交于点O,连接OE
在□ABCD中,AO=OC,BO=DO. 在 中,OE=
中,OE=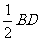 ,
,
在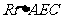 中,OE=
中,OE=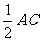 ,∴BD=AC, ∴□ABCD为矩形.
,∴BD=AC, ∴□ABCD为矩形.
1.C;2.D,提示:由勾股定理求得斜边为: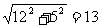 ,斜边的中线长为
,斜边的中线长为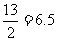 ;3.18,提示:AB=5,BC=12,AC=13,
;3.18,提示:AB=5,BC=12,AC=13,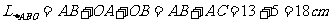 ;4. A,提示:DE=3,AB=AE=6,在直角三角形ADE中,∠DAE=30
;4. A,提示:DE=3,AB=AE=6,在直角三角形ADE中,∠DAE=30 ,由折叠的性质得∠BAF=∠EAF=30,设BF=
,由折叠的性质得∠BAF=∠EAF=30,设BF= ,则AF=2
,则AF=2 ,
,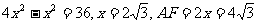 ;5.3;6.14;
;5.3;6.14;
7证明:∵四边形ABCD为矩形,∴AC=BD,BO=CO,
∵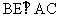 ,
,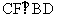 ,∴∠BEO=∠CFO=90
,∴∠BEO=∠CFO=90 ,又∵∠BOE=∠COF
,又∵∠BOE=∠COF
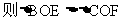 ∴BE=CF
∴BE=CF
10.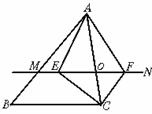 如图所示,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
如图所示,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

课时一答案:
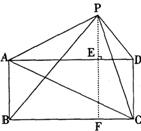
9.已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
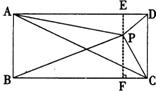
图l
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴ S△PBC+S△PAD= S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、SPCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
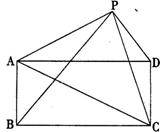

图2 图3
8.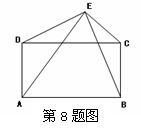 如图所示,E为□ABCD外,AE⊥CE,BE⊥DE,
如图所示,E为□ABCD外,AE⊥CE,BE⊥DE,
求证:□ABCD为矩形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com