3．如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是(　)

A．∠M＝∠N　B．AB＝CD　C．AM＝CN　　D．AM∥CN

2．(2004·山东潍坊市)如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是　　　　　　　(　 )

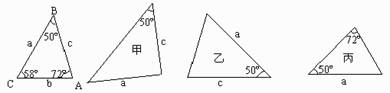
A．甲和乙　 　B．乙和丙　 　C．只有乙　 　D．只有丙

1．如图,已知AC和BD相交于O,且BO＝DO,AO＝CO,下列判断正确的是(　)

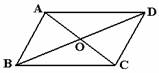A．只能证明△AOB≌△COD　

B．只能证明△AOD≌△COB

C．只能证明△AOB≌△COB　

D．能证明△AOB≌△COD和△AOD≌△COB

11. 解：(1)如图1，连结DF．

　　 因为点E为CD的中点，所以．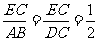

　　 据题意可证△FEC∽△FBA，所以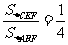．　 (2分)

　　 因为S_△DEF=S_△CEF，S_△=S．　 　　　　　　　　(2分)

　　 所以．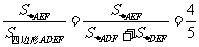　　　

　　 (2)如图2，连结DF．

　 与(1)同理可知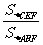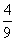，=，S_△DEF=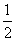S_△CEF，，

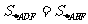　　 所以=．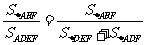　　　　　

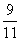　　 (3)当CE：ED=3：1时，=．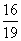　　

　　 当CE：ED=n：1时， =(=)．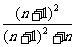　　　　

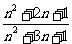　　 (4)提问举例：①当点E运动到CE：ED=5：1时，△ABF与四边形ADEF的面积之比是多少？

　　 ②当点E运动到CE：ED=2：3时，△ABF与四边形ADEF的面积之比是多少？

　　 ③当点E运动到CE：ED=m：n(m，n是正整数)时，△ABF与四边形ADEF的面积之比是多少？

10. 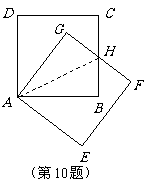解：．

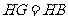证法1：连结，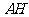

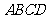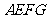四边形，都是正方形．

．

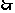
由题意知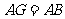，又．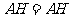

，

．

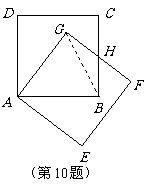
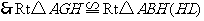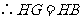证法2：连结．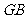

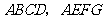四边形都是正方形，

．

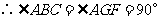由题意知．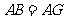

．

．

．

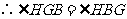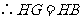9. (1) 证明： 如图，∵ AD=CD，DE=DG，∠ADC=∠GDE=90^o，　　　　　　　

又 ∠CDG=90^o +∠ADG=∠ADE，　

∴ △ADE≌△CDG． ∴ AE=CG．　

(2)猜想： AE⊥CG．

证明： 如图，

设AE与CG交点为M，AD与CG交点为N．　　

∵ △ADE≌△CDG， ∴ ∠DAE=∠DCG．　 　

又∵ ∠ANM=∠CND， ∴ △AMN∽△CDN．　

∴ ∠AMN=∠ADC=90^o．∴ AE⊥CG．　　　

8.证明：(1)∵四边形ABCD是正方形.∴BC=DC，∠BCD=90°

在Rt△BCE和Rt△DCF中，BC=DC，CE=CF,∴Rt△BCE≌Rt△DCF

(2)∵CE=CF，∴∠CEF=∠CFE,∴∠CFE=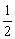(180°－90°)=45°

∵Rt△BCE≌Rt△DCF,∴∠CFD=∠BEC=60°

∴∠EFD=∠DFC－∠EFC=15°

6. 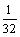;7.105;

1.A；2.A; 3.∠A=90°或∠B=90°或∠C=90°或∠D=90°中的任一条件即可;4. D；5. 3；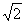

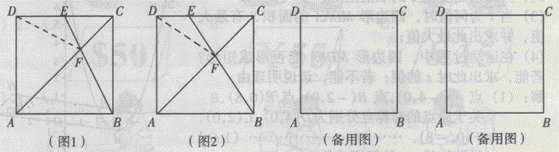
11.如图，点E在正方形ABCD的边CD上运动，AC与BE交于点F．

　　 (1)如图1，当点E运动到DC的中点时，求△ABF与四边形ADEF的面积之比；

　　 (2)如图2，当点E运动到CE：ED=2：1时，求△ABF与四边形ADEF的面积之比．

　　 (3)当点E运动到CE：ED=3：1时，写出△ABF与四边形ADEF的面积之比；当点E运动到CE：ED=n：1(n是正整数)时，猜想△ABF与四边形ADEF的面积之比(只写结果，不要求写出计算过程)；

(4)请你利用上述图形，提出一个类似的问题(根据提出的问题给附加分，最多4分，计入总分，但总分不超过120分)．

课时三答案：