
19.2.1 矩形(二)
|
教学目标 |
知识与技能 |
1.理解并掌握矩形的判定方法. 2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力 |
|
过程与方法 |
经历探索矩形判定的过程,发展学生实验探索的意识;形成几何分析思路和方法. |
|
|
情感态度与价值观 |
培养推理能力,会根据需要选择有关的结论证明,体会来自于实践的需要. |
|
|
重点 |
矩形的性质定理1、2及推论. |
|
|
难点 |
定理的证明方法及运用. |
教 学 过 程
|
备 注 |
教学设计 与 师生互动 |
|
|
第一步:课堂引入 1.什么叫做平行四边形?什么叫做矩形? 2.矩形有哪些性质? 3.矩形与平行四边形有什么共同之处?有什么不同之处? 4.事例引入:小华想要做一个矩形像框送给妈妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行? 总结:矩形的判定方法. 矩形判定方法1:对角钱相等的平行四边形是矩形. 矩形判定方法2:有三个角是直角的四边形是矩形. 推论:直角三角形斜边的中线是斜边的一半. (指出:判定一个四边形是矩形,知道三个角是直角,条件就够了.因为由四边形内角和可知,这时第四个角一定是直角.) 反馈归纳 (1)矩形判定定理1:有三个角是直角的四边形是矩形. 已知:在四边形ABCD中,∠A=∠B=∠C=900, 求证:四边形ABCD是矩形. (方法指导:有一个角是900的平行四边形是矩形.) (2)矩形判定定理2:对角线相等的平行四边形是矩形. 已知:在平行四边形ABCD中,AC=DB, 求证:平行四边形ABCD是矩形. (方法指导:平行四边形的邻角互补,同时三角形全等,邻角相等) (3)小结:用定义判定矩形,与定理1、定理2从条件的个数上有何区别? 定义:有一个角是直角平行四边形 定理1:三个角是直角四边形 定理2:对角线相等平行四边形  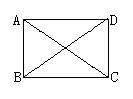 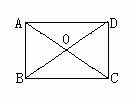 |
|
第二步:应用举例: 例1(补充)下列各句判定矩形的说法是否正确?为什么? (1)有一个角是直角的四边形是矩形; (×) (2)有四个角是直角的四边形是矩形; (√) (3)四个角都相等的四边形是矩形; (√) (4)对角线相等的四边形是矩形; (×) (5)对角线相等且互相垂直的四边形是矩形; (×) (6)对角线互相平分且相等的四边形是矩形; (√) (7)对角线相等,且有一个角是直角的四边形是矩形; (×) (8)一组邻边垂直,一组对边平行且相等的四边形是矩形;(√) (9)两组对边分别平行,且对角线相等的四边形是矩形. (√) 指出: (l)所给四边形添加的条件不满足三个的肯定不是矩形; (2)所给四边形添加的条件是三个独立条件,但若与判定方法不同,则需要利用定义和判定方法证明或举反例,才能下结论. 例2 (补充)已知  ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积. ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.分析:首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值. 解:∵ 四边形ABCD是平行四边形, ∴ AO=  AC,BO= AC,BO= BD. BD.∵ AO=BO, ∴ AC=BD. ∴  ABCD是矩形(对角线相等的平行四边形是矩形). ABCD是矩形(对角线相等的平行四边形是矩形).在Rt△ABC中, ∵ AB=4cm,AC=2AO=8cm, ∴ BC= 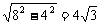 (cm). (cm). 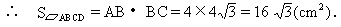 例3 (补充) 已知:如图(1),  ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形. ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.分析:要证四边形EFGH是矩形,由于此题目可分解出基本图形,如图(2),因此,可选用“三个角是直角的四边形是矩形”来证明. 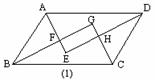 证明:∵ 四边形ABCD是平行四边形, 证明:∵ 四边形ABCD是平行四边形,∴ AD∥BC. ∴ ∠DAB+∠ABC=180°.  又
AE平分∠DAB,BG平分∠ABC
, 又
AE平分∠DAB,BG平分∠ABC
,∴ ∠EAB+∠ABG=  ×180°=90°. ×180°=90°. ∴ ∠AFB=90°. ∴ ∠AFB=90°.同理可证 ∠AED=∠BGC=∠CHD=90°. ∴ 四边形EFGH是平行四边形(有三个角是直角的四边形是矩形). |
|
|
第三步:随堂练习: 1.(选择)下列说法正确的是( ). (A)有一组对角是直角的四边形一定是矩形(B)有一组邻角是直角的四边形一定是矩形 (C)对角线互相平分的四边形是矩形 (D)对角互补的平行四边形是矩形 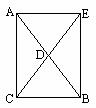 2.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形. 2.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.3、(1)有一组对角是直角的四边形一定是矩形.( ) (2)有一组邻角是直角的四边形一定是矩形.( ) (3)对角线互相平分的四边形是矩形.( ) (4)对角互补的平行四边形是矩形.( ) (5)有三个角是 是矩形,有一个角是 是矩形. (6)两组对边分别平行,且对角线 的四边形是矩形. 创新练习题 (1)满足下列条件( )的四边形是矩形. (A)有三个角相等 (B)有一个角是直角 (C)对角线相等且互相垂直 (D)对角线相等且互相平分 达标练习题 (1)已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形. 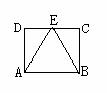 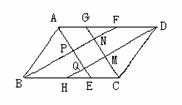 (2)回答:怎样用刻度尺,检查一个四边形是不是矩形. 综合应用练习 已知:如图,平行四边形ABCD的内角平分线交于点P、Q、M、N,求证:四边形PQMN是矩形. |
|
|
第四步:课后练习 1.工人师傅做铝合金窗框分下面三个步骤进行: ⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH; ⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ; ⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ; 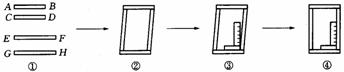 2.在Rt△ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数. |
|
|
第五步:小结 矩形的判定方法分两类:从四边形来判定和从平行四边形来判定. 常用的判定方法有三种:定义和两个判定定理.遇到具体题目,可根据条 件灵活选用恰当的方法. |
|
|
课后反思 : |
19.2.1 矩形(一)
|
教学目标 |
知识与技能 |
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系. 2.会初步运用矩形的概念和性质来解决有关问题. |
|
过程与方法 |
经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思维方法.并 渗透运动联系、从量变到质变的观点. |
|
|
情感态度与价值观 |
培养严谨的推理能力,以及自主合的精神,体会逻辑推理的思维价值. |
|
|
重点 |
矩形的性质. |
|
|
难点 |
矩形的性质的灵活应用. |
教 学 过 程
|
备 注 |
教学设计 与 师生互动 |
|
|
第一步:课堂引入 1.展示生活中一些平行四边形的实际应用图片(推拉门,活动衣架,篱笆、井架等),想一想:这里面应用了平行四边形的什么性质? 2.思考:拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?(动画演示拉动过程如图) 3.再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形?(小学学过的长方形)引出本课题及矩形定义. 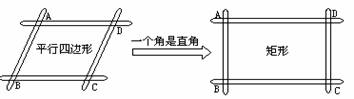 矩形定义:有一个角是直角的平行四边形叫做矩形(通常也叫长方形). 矩形是我们最常见的图形之一,例如书桌面、教科书的封面等都有矩形形象. [探究]在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状. ① 随着∠α的变化,两条对角线的长度分别是怎样变化的? ② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系? 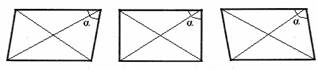 操作,思考、交流、归纳后得到矩形的性质. 矩形性质1 矩形的四个角都是直角. 矩形性质2 矩形的对角线相等. 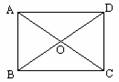 如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO= 如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=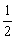 AC= AC=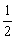 BD. BD.因此可以得到直角三角形的一个性质: 直角三角形斜边上的中线等于斜边的一半. |
|
第二步:应用举例: 例1 (教材P104例1)已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长. 分析:因为矩形是特殊的平行四边形,所以它具有对角线相等且互相平分的特殊性质,根据矩形的这个特性和已知,可得△OAB是等边三角形,因此对角线的长度可求. 解:∵ 四边形ABCD是矩形, ∴ AC与BD相等且互相平分. ∴ OA=OB. 又 ∠AOB=60°, ∴ △OAB是等边三角形. ∴ 矩形的对角线长AC=BD = 2OA=2×4=8(cm). 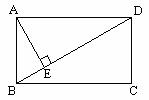 例2(补充)已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长. 例2(补充)已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长.分析:(1)因为矩形四个角都是直角,因此矩形中的计算经常要用到直角三角形的性质,而此题利用方程的思想,解决直角三角形中的计算,这是几何计算题中常用的方法. 略解:设AD=xcm,则对角线长(x+4)cm,在Rt△ABD中,由勾股定理: 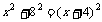 ,解得x=6. 则 AD=6cm. ,解得x=6. 则 AD=6cm.(2)“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×DB= AD×AB,解得 AE= 4.8cm. 例3(补充) 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF. 分析:CE、EF分别是BC,AE等线段上的一部分,若AF=BE,则问题解决,而证明AF=BE,只要证明△ABE≌△DFA即可,在矩形中容易构造全等的直角三角形. 证明:∵ 四边形ABCD是矩形, 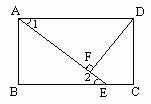 ∴ ∠B=90°,且AD∥BC. ∴ ∠B=90°,且AD∥BC. ∴ ∠1=∠2. ∵ DF⊥AE, ∴ ∠AFD=90°. ∴ ∠B=∠AFD.又 AD=AE, ∴ △ABE≌△DFA(AAS). ∴ AF=BE. ∴ EF=EC. 此题还可以连接DE,证明△DEF≌△DEC,得到EF=EC. 例2 已知:如图3,矩形ABCD中, 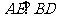 于E,且 于E,且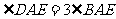 . .求: 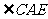 的度数. 的度数.分析:由已知 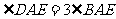 可得 可得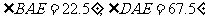 .而所求 .而所求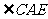 是 是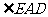 的一部分,就要研究 的一部分,就要研究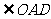 与其它角的关系.因为OA=OD,所以 与其它角的关系.因为OA=OD,所以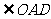 = =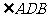 .把题目中的已知条件 .把题目中的已知条件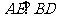 ,与矩形的性质 ,与矩形的性质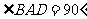 结合起来,得到基本图形直角三角形斜边上的高的形式,可以推出 结合起来,得到基本图形直角三角形斜边上的高的形式,可以推出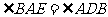 ,于是得到 ,于是得到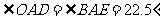 ,求 ,求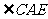 的度数也就显然了. 的度数也就显然了.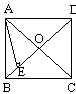 图3 解: 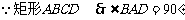 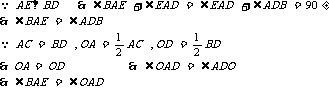 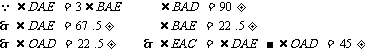 例3 已知:如图4,矩形ABCD的对角线AC、BD交于O,EF过O点交AD于E,交BC于F,且EF=BF, 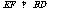 .求证:CF=OF. .求证:CF=OF.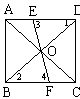 图4 分析:欲证CF=OF,只要  ,由矩形可知 ,由矩形可知 .由 .由 ,可得到OE=OF,又因为EF=BF,有 ,可得到OE=OF,又因为EF=BF,有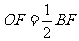 ,由于 ,由于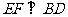 ,于是 ,于是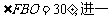 步 步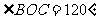 ,又有 ,又有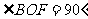 , ,  |
|
|
第三步:随堂练习 1.(填空) (1)矩形的定义中有两个条件:一是 ,二是 . (2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 . (3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm. 2.(选择) (1)下列说法错误的是( ). (A)矩形的对角线互相平分 (B)矩形的对角线相等步为营 (C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形 (2)矩形的对角线把矩形分成的三角形中全等三角形一共有( ). 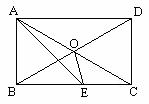 (A)2对 (B)4对
(C)6对 (D)8对 (A)2对 (B)4对
(C)6对 (D)8对3.已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO的度数. 3. 如图5,在矩形ABCD中, 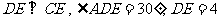 ,求这个矩形的周长.(答案:16+ ,求这个矩形的周长.(答案:16+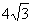 ) )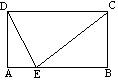 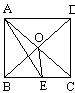 图5 图6 在矩形中若存在矩形对角线,那就一定要利用矩形对角线的性质,即相等又平分,转化成等腰三角形,利用等边对等角的性质. 4、 已知:如图6,矩形ABCD中,AE平分 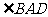 交BC于E,若 交BC于E,若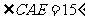 求: 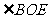 的度数.(提示:要充分利用等腰 的度数.(提示:要充分利用等腰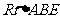 ,等边 ,等边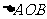 的性质) 的性质)解:  矩形ABCD,AE平分 矩形ABCD,AE平分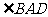  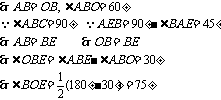 |
|
|
第四步:课后练习 1.(选择)矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ). (A)12cm (B)10cm (C)7.5cm (D)5cm 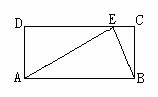 2.在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数. 2.在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.3.已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED. 4.如图,矩形ABCD中,AB=2BC,且AB=AE,求证:∠CBE的度数. |
|
|
课后小结与反思: 今天我们主要学习了矩形的定义及性质,矩形是角特殊的平行四边形,决定了矩形的四个角都是直角,对角线相等.由于矩形的对角线把矩形分割成直角三角形,等腰三角形,所以我们还要把直角三角形,等腰三角形,等边三角形的性质、判定好好复习一下,这对于解决矩形问题是大有好处的. |
 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。
小结
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?
 练习1、已知:如图,AD∥BC,AD=CB.
练习1、已知:如图,AD∥BC,AD=CB.
|
|
练习2、已知:如图,AD∥BC,AD=BC,AE=CF.
 求证:△AFD≌△CEB
求证:△AFD≌△CEB
练习3、已知:如图,AB=AC,AD=AE, ∠1=∠2.
求证:△ADB≌△ACE
练习1、如图,下列哪组条件不能判定△ABC≌△DEF( )

练习2、已知:如图,AC=AD, ∠CAB=∠DAB
 求证:△ACB≌△ADB
求证:△ACB≌△ADB
练习3、已知:如图,AB=AC,AD=AE.
求证: △ABE≌△ACD
画一个△ABC,使AB=5cm,AC=3cm。
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
三角形全等判定方法1:
用符号语言表达为:
全等三角形的性质是什么?
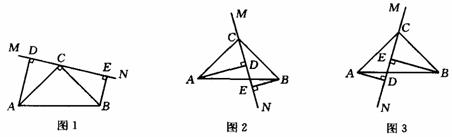
 如:△ABC≌△DEF,可以写出以下推理:
如:△ABC≌△DEF,可以写出以下推理:
15.在△ABC中,∠ACB=90o,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
⑴当直线MN绕点C旋转到图⑴的位置时,求证:①△ACD≌△CEB;②DE=AD+BE
⑵当直线MN绕点C旋转到图⑵的位置时,求证:DE=AD-BE;
⑶当直线MN绕点C旋转到图⑶的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
注意:第(2)、(3)小题你选答的是第 小题.
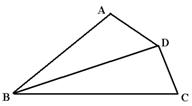
14.如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180o,试说明AD=CD.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com