例1.①求出如图所示的Rt△ABC中，∠A的四个三角函数值。

解：Rt△ABC中，AB=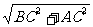==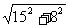17　　　　　　　

　　 ∴sinA=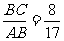，cosA=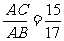　　　　　　　　　　　　　　　　　　

　　　 tanA=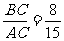，cotA=　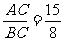　　　　　　　　　　　　　 8

②若图中AC︰BC=4︰3呢？　　　　　　　　　　　　　　　 15

解：设AC=4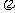，BC=3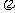，则AB=5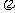　　　　　　　　　　

　　 ∴sinA=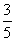，cosA=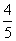，tanA=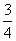，cotA=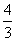

③若图中tanA=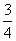呢？(解法同上)

例2.△ABC中，∠B=90°，a=5，b=13，求∠A的四个三角函数值。　

解：Rt△ABC中，c===12　　　　 　　　　　　　　　

∴sinA=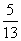，cosA=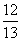，tanA=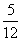，cotA=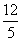　　　　　　　

注意：解Rt△，如无图，应根据题意自己画图，寻找线段比值也应根据定义，不能死记公式。

4.四种三角函数的关系。

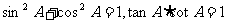
3.四种锐角三角函数。

分别叫做锐角∠A的正弦、余弦、正切、余切，统称为锐角∠A的三角函数.

显然，锐角三角函数值都是正实数，并且0<sinA<1,0<cosA<1,tanA>0,cotA>0.

2.如图，由Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3

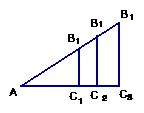得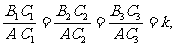

可见，在Rt△ABC中，对于锐角A的每一

个确定的值，其对边与邻边的比值是惟一确定的。

同样，其对边与斜边，邻边与斜边，邻边与对边的比值也是惟一确定的。

1.Rt△ABC中，某个角的对边、邻边的介绍。

2.Rt△中角、边之间的关系是：①∠A+∠B=90°②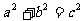

1.　　　 什么叫Rt△？它的三边有何关系？

6.课外作业与拓展

参见励耘精品系列丛书《课时导航》华师大版八年级(下)P50－P51

5.回顾联系，形成结构

(1)　　 锐角的三角函数是指哪些？它们的定义分别是怎样的？

(2)　　 回顾30゜、45゜、60゜的三角函数值。

(3)　　 求三角函数值，根据定义式，可转化为求一些有关的边长。

4.课内深化，提升能力

(1)如图，在Rt△MNP中，∠N＝90゜.

∠P的对边是__________,∠P的邻边是_______________;

　∠M的对边是__________,∠M的邻边是_______________;

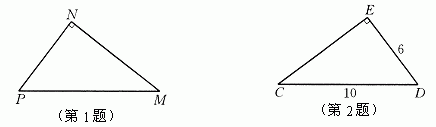
(2)求出如图所示的Rt△DEC(∠E＝90゜)中∠D的四个三角函数值.

(3)设Rt△ABC中，∠C＝90゜，∠A、∠B、∠C的对边分别为a、b、c，根据下列所给条件求∠B的四个三角函数值.

1)a=3,b=4;　　　　　 　2)a=6,c=10.

(4)求下列各式的值.

　1)sin30゜+sin²45゜-tan²60゜;

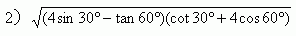
　3)2cos60゜+2sin30゜+4tan45゜.

(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P51第18题)

(5)在Rt△ABC中，∠C＝90゜，已知AC＝21，AB＝29，分别求∠A、∠B的四个三角函数值.

(6)在Rt△ABC中，∠C＝90゜，BC:AC＝5:12，求∠A的四个三角函数值.

　 　(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P51第15题)