1.　　 △ABC中，∠C=90°，a=40,c=41.

求的值。　　　　　 (　　 0　　 )

2.　　 利用同角三角函数中的平方关系式

解法一：设a=，c=，则b=，∴cosA=

解法二：∵sin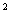A+cos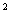A=1，sinA=，∴cosA=

三。引申提高：

例3.如图，在Rt△ABC中，∠ACB=90°，sinB=，D是BC上一点，DE⊥AB于E，CD=DE，AC+CD=9，求BE、CE的长。

分析：由sinB=　 ，可设DE=CD= ，DB=，则BC=8，AC=6，AB=10，再由AC+CD=9，可求出各边长。在Rt△BDE中，由勾股定理求BE长，过C作CF⊥AB，再用勾股定理求解。

解：∵sinB=，∠ACB=90°，DE⊥AB，∴sinB=，设DE=CD=3，则DB=5

又CD=DE=3，∴CB=8，∴AC=6，AB=10，∵AC+CD=9，∴6，∴

∴DE=3，DB=5，∴BE=

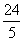过C作CF⊥AB于F，则CF∥DE，∴，求得CF=，BF=

∴EF=，在Rt△CEF中，

例1.如图，菱形ABCD中，对角线AC=16，BD=30，求:①∠ABD的四个三角函数值。②sin∠ABC

解：①在菱形ABCD中，AO=CO=8，BO=DO=15，AC⊥BD，∴AB===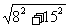17

在Rt△ABO中，sin∠ABD=，cos∠ABD=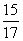，tan∠ABD=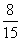，cot∠ABD=

②过C作CE⊥AB于E，菱形ABCD中，AB=BC=17，S=

　 　　∴×16×30=，∴CE=

Rt△BCE中，sin∠ABC=

例2.在△ABC中，∠C=90°，sinA=，求cosA的值

分析：本题可有两种方法求解

1.　　 利用∠A的正弦、余弦的定义来解

3.　　 练习：书P习题19.3　 1-5　

2.　　 特殊三角的三角函数值

1.　　 直角三角形中四个锐角三角函数的求法

　　 《创新教育目标手册》 P.95。课内练习　 1-4　 A组 1-4

灵活运用四个三角函数求值。

例3．如图，∠ACB=90°，CD⊥AB于D，若AD=2，BD=8。

求cosB。你还能求什么？　　　　　　　　　　　　　　　　　　

法一：Rt△BCD,　　　　　　　

法二：Rt△ABC中，

变式：若AD:BD=9:16, 求∠A的四个三角函数值。　　　 (　 　)

书P1-3