
 (与学生共同梳理、总结梯形的判定方法及添加辅助线的解决有关梯形问题的常用方法)
(与学生共同梳理、总结梯形的判定方法及添加辅助线的解决有关梯形问题的常用方法)
等腰梯形的判定方法:
(1)两腰相等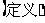
(2)同底上的两个角相等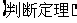
梯形的画法:画出符合条件的梯形,通常先要“分析”,借助铺线找出可以画出的部分图形(等腰三角形,直角三角形等).
梯形中常用的四种辅助线的添法(如下图):
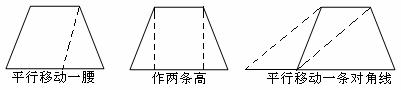
1;课本P119练习3,4.
2,参看列1:证法三.
2,画法:参看补充题.
腰长=
周长=2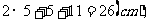
面积=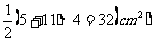
2、补充练习.
(1)等腰梯形与等腰三角形有哪些联系?
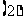 有两各内角是70
有两各内角是70 得梯形一定是等腰梯形?为什么?
得梯形一定是等腰梯形?为什么?
受刚才做图的启发:只有等腰三角形才能得到等腰梯形。请同学们靠虑下面的问题。
议一议:
“在同一底上的两个角相等的梯形是等腰梯形”这个命题成立吗?能否加以证明。
学生活动:
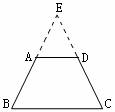 (通过想一想,试一试,议一议。做一做的小活动,初步懂得添加辅助线的一般方法,学会将梯形问题转化为平行四边形、矩形、等腰三角形来处理)
(通过想一想,试一试,议一议。做一做的小活动,初步懂得添加辅助线的一般方法,学会将梯形问题转化为平行四边形、矩形、等腰三角形来处理)
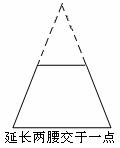
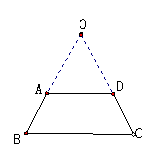
证法一:如图延长BA.CD相交于点E.
∵∠B=∠C(三角形中等角对边等)
∴BE=CE.
∵四边形ABCD是梯形,
 ∴AD∥BC.
∴AD∥BC.
∴∠EAD=∠B,∠EDA=∠C.
即AB=CD,
∴梯形ABCD是等腰梯形.
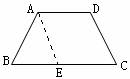
证法二: 如图将CD平移到AE位置.
此时四边形AECD是平行四边形.
则AE∥CD且AE=CD,
∴∠AEB=∠C.
又∵∠B=∠C,
∴∠B=∠AEB.
∴AB=AE.(三角形等角对边等)
∴AB=CD.
因此梯形ABCD是等腰梯形.
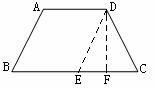
证法三: 如图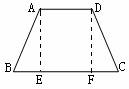 作梯形ABCD的高AE、DF分别交于BC于E、F.
作梯形ABCD的高AE、DF分别交于BC于E、F.
∵梯形上、下底平行,即AD∥BC,
∴AE=DF.(夹在平行线间的垂线段相等)
又∵∠AEB=∠DFC=90°,∠B=∠C,
∴△ABE≌△DCF.
∴AB=DC
∴梯形ABCD是等腰梯形.
通过活动,同学的说理能力以有了很大提高。由此我们也得到等腰梯形的两种判定方法。
(1) 两腰相等的梯形是等腰梯形。
(2) 同一底上两个角相等的梯形是等腰梯形。
应用举例:
[列2]如下图,梯形ABCD中,BC∥AD,DC∥AB.DE=DC,∠A=100°,求梯形其他三个内角的度数.
师生共析:
(1) 梯形上、下底平行,可以由同旁内角互补求得∠B=80°
(2) 可想办法证明梯形ABCD是等腰梯形,从而解决∠C和∠ADC的问题.
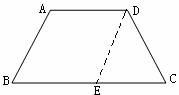 解:∵BC∥AD,DE∥AB,
解:∵BC∥AD,DE∥AB,
∴四边形ABED是平行四边形.
∴AB=DE.
又DE=DC
∴AB=DC.
梯形ABCD是等腰梯形,
∴∠C=∠B=180°-∠A=80°,
∠D=∠A=100°.
补充题:画一个等腰梯形,使它的上.下底分别为4cm和10cm,高为3cm.
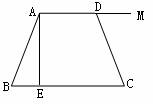 分析:假设等腰梯形ABCD已画出,如下图,作出高AE和DF,可证得Rt△ABE Rt△DCF,所以EF=AD=4cm,BE=CF=
分析:假设等腰梯形ABCD已画出,如下图,作出高AE和DF,可证得Rt△ABE Rt△DCF,所以EF=AD=4cm,BE=CF=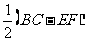 =3cm.于是可先画出Rt△ABE,进而确定点C,过A作AD∥BC,使AD=4cm,可确定D,连接DC,即可确定等腰梯形ABCD.
=3cm.于是可先画出Rt△ABE,进而确定点C,过A作AD∥BC,使AD=4cm,可确定D,连接DC,即可确定等腰梯形ABCD.
画法:(1)画Rt△ABE使∠AEB=90°,AE=3cm,BE=3cm.
(2)延长BE到C使BC=10cm.
(3)过A作AM∥BC,且使BC、AM在AB的同旁,在AM上截取AD=10cm.
(4)连接DC,则梯形ABCD就是所要画的等腰梯形.(如图)
(还可以启发学生思考、讨论,得多种画法)
如左下图,平行移动一腰AB到DF,可在Rt△CDF中算出腰CD的长,CD=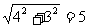 (cm),因此可先画出等腰△DCE,从而画出等腰梯形ABCD;又如右下图利用等腰梯形轴对称图形,且对称轴是连结上、下两底中点的线段所在的直线.因此可以先画梯形ABEF使EF=3cm,EF⊥BE,BE=6cm,AF∥BE.然后利用轴对称性画
(cm),因此可先画出等腰△DCE,从而画出等腰梯形ABCD;又如右下图利用等腰梯形轴对称图形,且对称轴是连结上、下两底中点的线段所在的直线.因此可以先画梯形ABEF使EF=3cm,EF⊥BE,BE=6cm,AF∥BE.然后利用轴对称性画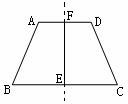
 出等腰梯形ABCD.
出等腰梯形ABCD.
上节课,我们研究了梯形,并且研究了特殊的梯形-等腰梯形的概念及其性质,请同学们说出什么样的梯形是等腰梯形?两腰梯形有什么性质?
(学生讨论)等腰梯形是特殊的梯形,所以它具有梯形的性质,它还具有下列一般梯形所不具备的性质.同一底上两个内角相等;对角线相等;是轴对称图形.
下面请同学们来做一做(老师播放课件,学生进行画、讨论、总结)
在下图中的每个三角形中画一条线段.
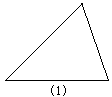
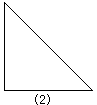
(1) 怎样画才能得到一个梯形?
(2) 在哪些三角形中,能够得到一个等腰梯形呢?
(1) 因为梯形的上、下两底平行且不相等,所以只要在三角形的两边上各找一点,使这两点的连线平行于第三边即可得到梯形。
(2) 第(2)(3)个三角形中能够得到一个等腰梯形。在等腰三角形的两腰上分别找一点,使这两点的连线平形于等腰三角形的底边即可得到一个等腰梯形。
(3) 说得太好了,这节课,我们就来探讨等腰梯形的判定。
4.梯形、多边形面积的计算
小学学过的梯形面积S=(a+b)h÷2 ,而l=(a+b)÷2,推出S=lh(l为梯形中位线长,h为梯形高).
多边形面积的求法,任意多边形面积可以通过辅助线,把它分割成三角形、平行四边形、梯形,就可以利用这些图形的面积公式计算任意多边形面积.
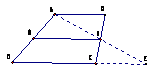 例1:课本P121习题第9题(让学生思考并寻求证明方法,教师加以巡视及点拨.)
例1:课本P121习题第9题(让学生思考并寻求证明方法,教师加以巡视及点拨.) ,且有MN∥BC∥AD
,且有MN∥BC∥AD 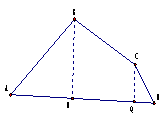 例2 有一块四边形的地ABCD, 测得AB=26m,BC=10m,CD=5m,顶点B、C到AD的距离分别为10m、4m,求这块地的面积.
例2 有一块四边形的地ABCD, 测得AB=26m,BC=10m,CD=5m,顶点B、C到AD的距离分别为10m、4m,求这块地的面积.19.3 梯形(三)
|
教学目标 |
知识与技能 |
使学生掌握梯形中位线定理,并能熟练地用它进行有关的论证和计算,进一步提高学生分析问题、解决问题的能力,培养学生具有“类比”和“转化”的数学思想和应用意识. |
|
过程与方法 |
经历探索会运用梯形的中位线和性质进行有关问题的论证和计算. |
|
|
情感态度与价值观 |
通过探索梯形的中位线的性质,提升学生的对知识的横向联系的素质 |
|
|
重点 |
梯形中位线性质及其证明. |
|
|
难点 |
任意多边形面积的计算. |
教学过程
|
备 注 |
教学设计 与 师生互动 |
||
|
|
第一步:复习提问 1.什么叫做三角形的中位线?它有什么性质? 2.等边三角形各边中点的连线形成什么图形? 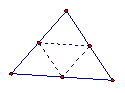 , ,3.梯形也有中位线.那么梯形的中位线及性质是什么? |
||
|
第二步:讲授新课: 1.梯形中位线:连结梯形两腰中点的线段叫做梯形的中位线. 强调:梯形中位线是连结两腰中点的线段,而不是连结两底中点的线段. 2.梯形中位线定理 梯形中位线平行于两底,并且等于两底和的一半. 该定理的证明关键是如何添加辅助线,把梯形中位线转化成三角形的中位线. 设法把梯形中位线转化为三角形中位线. 3. 等腰梯形的常用辅助线的添加方法 作法一:过点C作CF∥AD交AB延长线于F 作法二:过A作AF⊥DC于F,BE⊥DC于E 作法三:延长DA、CB交于点O 作法四: 过点B作 BE∥AD,交DC于点 
作法五:过点B作BE∥AC交DC延长线于点E 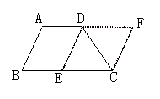 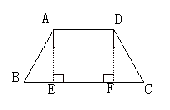
作法一 作法二
作法三 作法四
作法五 3.做-做--探索等腰梯形的性质(引入用轴对称解决问题的思想). 在一张方格纸上作一个等腰梯形,连接两条对角线. [问题一] 图中有哪些相等的线段?有哪些相等的角?这个图形是轴对称图形吗?学生画图并通过观察猜想; [问题二] 这个等腰梯形的两条对角线的长度有什么关系? 结论: ①等腰梯形是轴对称图形,上下底的中点连线是对称轴. ②等腰梯形同一底上的两个角相等. ③等腰梯形的两条对角线相等. 解决梯形问题常用的方法: (1)“平移腰”:把梯形分成一个平行四边形和一个三角形(图1); (2)“作高”:使两腰在两个直角三角形中(图2); (3)“平移对角线”:使两条对角线在同一个三角形中(图3); (4)“延腰”:构造具有公共角的两个等腰三角形(图4); (5)“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形(图5).
图1 图2 图3 图4 图5 综上所述:解决梯形问题的基本思想和方法就是通过添加适当的辅助线,把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决. |
|||
第三步;应用举例: 例1(教材P118的例1)略. 例1(教材P118的例1)略. (延长两腰 梯形辅助线添加方法三) (延长两腰 梯形辅助线添加方法三)例2(补充)如图,梯形ABCD中,AD∥BC, ∠B=70°,∠C=40°,AD=6cm,BC=15cm. 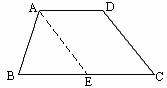 求CD的长. 求CD的长.分析:设法把已知中所给的条件都移到一个三角形中,便可以解决问题.其方法是:平移一腰,过点A作AE∥DC交BC于E,因此四边形AECD是平行四边形,由已知又可以得到△ABE是等腰三角形(EA=EB),因此CD=EA=EB=BC-EC=BC-AD=9cm. 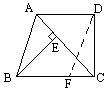 解(略).
解(略).例3 (补充) 已知:如图,在梯形ABCD中,AD∥BC,∠D=90°,∠CAB=∠ABC, BE⊥AC于E.求证:BE=CD. 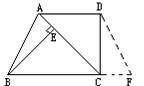 分析:要证BE=CD,需添加适当的辅助线,构造全等三角形,其方法是:平移一腰,过点D作DF∥AB交BC于F,因此四边形ABFD是平行四边形,则DF=AB,由已知可导出∠DFC=∠BAE,因此Rt△ABE≌Rt△FDC(AAS),故可得出BE=CD.
分析:要证BE=CD,需添加适当的辅助线,构造全等三角形,其方法是:平移一腰,过点D作DF∥AB交BC于F,因此四边形ABFD是平行四边形,则DF=AB,由已知可导出∠DFC=∠BAE,因此Rt△ABE≌Rt△FDC(AAS),故可得出BE=CD.证明(略) 另证:如图,根据题意可构造等腰梯形ABFD,证明△ABE≌△FDC即可. 例4:求证:等腰梯形的两条对角线相等 已知: 求证: 例5:如图4.9-4,梯形ABCD中,AD∥BC,∠B=70°,∠C=40°,AD=6cm,BC=15cm,求CD的长. 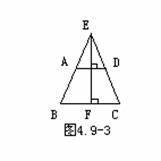 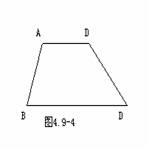 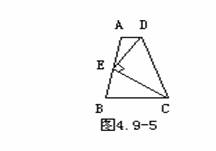 例6:已知等腰梯形的锐角等于60°它的两底分别为15cm和49cm,求它的腰长. 已知: 求证: 例4:已知:如图4.9-5,梯形ABCD中,AD∥BC,E是AB的中点,DE⊥CE,求证:AD+BC=DC. |
|||
|
第四步:课堂练习 1、填空 (1)在梯形ABCD中,已知AD∥BC,∠B=50°,∠C=80°,AD=a,BC=b,,则DC= . (2)直角梯形的高为6cm,有一个角是30°,则这个梯形的两腰分别是 和 . (3)等腰梯形 ABCD中,AB∥DC,A C平分∠DAB,∠DAB=60°,若梯形周长为8cm,则AD= . 2、如图4.9-6,等腰梯形ABCD中,AB=2CD,AC平分∠DAB,AB= 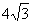 ,(1)求梯形的各角.(2)求梯形的面积. ,(1)求梯形的各角.(2)求梯形的面积.3、(1)在梯形ABCD中,已知AD∥BC,∠B=50°,∠C=80°,AD=a,BC=b,,则DC= . (2)直角梯形的高为6cm,有一个角是30°,则这个梯形的两腰分别是 和 . (3)等腰梯形 ABCD中,AB∥DC,A C平分∠DAB,∠DAB=60°,若梯形周长为8cm,则AD= .  4.已知:如图,在等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,BD平分∠ABC,∠A=60°,梯形周长是20cm,求梯形的各边的长. (AD=DC=BC=4,AB=8) 4.已知:如图,在等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,BD平分∠ABC,∠A=60°,梯形周长是20cm,求梯形的各边的长. (AD=DC=BC=4,AB=8)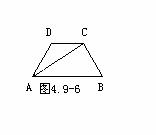 |
|||
|
第五步:课后练习 1.填空:已知直角梯形的两腰之比是1∶2,那么该梯形的最大角为 ,最小角为 . 2.已知等腰梯形的锐角等于60°它的两底分别为15cm和49cm,求它的腰长和面积. 3.已知:如图,梯形ABCD中,CD//AB, 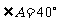 , ,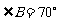 .求证:AD=AB-DC. .求证:AD=AB-DC.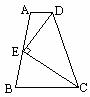 4.已知,如图,梯形ABCD中,AD∥BC,E是AB的中点,DE⊥CE,求证:AD+BC=DC.(延长DE交CB延长线于点F,由全等可得结论) 4.已知,如图,梯形ABCD中,AD∥BC,E是AB的中点,DE⊥CE,求证:AD+BC=DC.(延长DE交CB延长线于点F,由全等可得结论) |
|||
|
第六步:课堂小结 1、梯形的定义及分类 2、等腰梯形的性质: (1)具有一般梯形的性质:AD∥BC. (2)两腰相等:AB=CD. (3)两底角相等:∠B=∠C,∠A=∠D. (4)是轴对称图形,对称轴是通过上、下底中点的直线. (5)两条对角线相等:AC=BD. 两条对角线的交点在对称轴上. 两腰延长线的交点在对称轴上. |
|||
|
课后反思 : |
19.3 梯形(一)
|
教学目标 |
知识与技能 |
1. 知道梯形、等腰梯形、直角梯形的有关概念;能说出并证明等腰梯形的两个性质;等腰梯形同一底上的两个角相等;两条对角线相等. 2. 会运用梯形的有关概念和性质进行有关问题的论证和计算. 3. 通过添加辅助线,把梯形的问题转化成平行四边形或三角形问题,使学生体会图形变换的方法和转化的思想. |
|
过程与方法 |
经历探索梯形的有关性质、概念的过程,发展学生学习数学中的转换、化归思维方法,体会平移,轴对称的有关知识在梯形中应用. |
|
|
情感态度与价值观 |
增强主动探索意识,发展合情推理思维,体会逻辑思维训练在实际问题中的价值. |
|
|
重点 |
等腰梯形的性质及其应用. |
|
|
难点 |
解决梯形问题的基本方法(将梯形转化为平行四边形和三角形及正确运用辅助线),及梯形有关知识的应用. |
教学过程
|
备 注 |
教学设计 与 师生互动 |
||||||||||||||||||||
|
|
第一步:复习引导 平行四边形、矩形、菱形、正方形的性质
|
||||||||||||||||||||
|
平行四边形、矩形、菱形、正方形的判定
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||
|
第二步:课堂引入 1.创设问题情境--引出梯形概念. [观察](教材P117中的观察)右图中,有你熟悉的图形吗?它们有什么共同的特点? 2.画一画:在下列所给图中的每个三角形中画一条线段,  [思考](1)怎样画才能得到一个梯形? [思考](1)怎样画才能得到一个梯形?(2)在哪些三角形中,能够得到一个等腰梯形?
梯形 一组对边平行而另一组对边不平行的四边形叫做梯形. (强调:①梯形与平行四边形的区别和联系;②上、下底的概念是由底的长短来定义的,而并不是指位置来说的.) (1)一些基本概念(如图):底、腰、高.
腰:不平行的一组对边叫做梯形的腰. 高:两底间的距离叫做梯形的高. 直角梯形:一腰垂直于底的梯形叫做直角梯形. 等腰梯形:两腰相等的梯形叫做等腰梯形. (2)等腰梯形:两腰相等的梯形叫做等腰梯形. (3)直角梯形:有一个角是直角的梯形叫做直角梯形.
2、预习梯形的判定及应用。 1、习题19·3 1、2、6、9 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |