2．课前热身

　　 (1)在稿纸上任意画一条线段a和一个∠1，然后用刻度尺和量角器画一条线段AB=a，∠AOB=∠1．

　　 (2)你的这种画法必须要先知道什么？

1．复习导入

　　 以前，我们是怎样画一条线段等于已知线段、画一个角等于已知角的？

　　 学会线段、角的尺规画法及其和、差画法，认识角的画法的理论依据．

(四)作业习题3、4题.　

(三)小结请同学们自己对本课内容进行小结.

(二)新课

1.画线段的垂直平分线.

请同学们探索用直尺和圆规准确地画出一条线段的垂直平分线.

已知线段a，用直尺和圆规准确地画出已知线段a的垂直平分线.

解决这一问题，要利用好线段垂直平分线的性质.

请同学们讨论、探索、交流、归纳出具体的作图方法.

例1 已知底边及底边上的高作等腰三角形.

分析：要完成这个作图，先作出底边，再作底边的垂直平分线，取高，最后完成三角形.

已知：底边a、及底边上的高h.(画出两条线段a、h)

求作：△ABC，使得一底边为a、底边上的高为h.

作法：(略).

2.画直线的垂线.

请同学们探索用直尺和圆规准确地画出一条直线的垂线.

请同学们讨论、探索、交流、归纳出具体的作图方法.

实际上，画出一条直线的垂线，就是转化为画线段的垂直平分线.

例2 过直线外一点作直线的垂线.

已知：直线a、及直线a外一点A.(画出直线a、点A)

求作：直线a的垂线直线b，使得直线b经过点A.

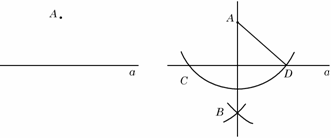
作法：(1)以点A为圆心，以适当长为半径画弧，交直线a于点C、D.

(2)以点C为圆心，以AD长为半径在直线另一侧画弧.

(3)以点D为圆心，以AD长为半径在直线另一侧画弧，交前一条弧于点B.　 (4)经过点A、B作直线AB.

直线AB就是所画的垂线b.(如图)

3.(优生)探索如何过一点、两点和不在同一直线上的三点作圆.

思考：如何解决这一实际问题?下面我们共同探寻解决这一问题的办法.

练习教材练习第1、2题.

探究1：过一个已知点A如何作圆?(如图，让学生动手去完成)

学生讨论并发现：过点A所作圆的圆心在哪儿?半径多大?可以作几个这样的圆?(圆心不定，半径不定，可以作无数个圆)

探究1　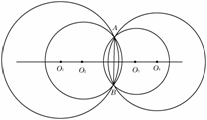 探究2　　　　　

探究2：过已知两点A、B如何作圆?(如图，学生动手去完成)

学生继续讨论并发现：它们的圆心到A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个?(OA=OB，圆心在直线AB的垂直平分线上，有无数个圆)

探究3：过同一平面内三个点的情况会怎样呢?

分两种情况研究：

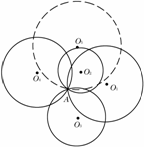
(1)求作一个圆，使它经过不在一直线上三点A、B、C.

已知：不在一直线上三点A、B、C，求作一个圆，使它同时经过点A、B、C.(学生口述作法，教师示范作图过程)

学生讨论并发现：这样一共可作几个圆?圆心在哪里?圆心到A、B、C三点的距离怎样?(可作一个圆，圆心是线段AB、AC、BC的垂直平分线的交点，圆心到A、B、C三点距离相等)

(2)过在一直线上的三点A、B、C可以作几个圆?(不能作出)

发现结论：不在同一直线上的三点确定一个圆：

(一)引入我们已熟悉尺规的两个基本作图：画线段，画角.

那么利用尺规还能解决什么作图问题呢?

3.尺规作图的简单应用，解尺规作图题，会写已知、求作和作法.

2.掌握尺规的基本作图：画线段的垂直平分线，画直线的垂线.

1.进一步熟练尺规作图.