
5.回顾联系,形成结构
如何借助计算器求一般角度的三角函数值,或已知某个角度的三角函数值求出该角的角度。
4.练习巩固,促进迁移
(1)用计算器求下式的值.(精确到0.0001)
sin81゜32′17″+cos38゜43′47″.
(2)已知cot A=3.1748,利用计算器求锐角A.(精确到1′)
(3)如图所示,在四边形ABCD中,AB=3,CD=1,∠A=60゜,∠B=∠D=90゜,求四边形ABCD的面积。
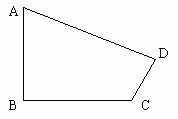
(此题选自励耘精品系列丛书《课时导航》华师大版八年级(下)P52第14题)
3.巩固应用,拓展研究
(1)使用计算器求下列三角函数值.(精确到0.0001)
sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.
(2)已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)
1)sin a=0.2476; 2)cos a=0.4174;
3)tan a=0.1890; 4)cot a=1.3773.
2.探索交流,概括方法
下面我们介绍如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角.
(1) 求已知锐角的三角函数值.
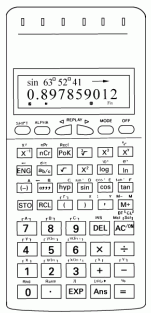
例1 求sin63゜52′41″的值.(精确到0.0001)
解 先用如下方法将角度单位状态设定为“度”:

再按下列顺序依次按键:

显示结果为0.897 859 012.
所以 sin63゜52′41″≈0.8979
例3 求cot70゜45′的值.(精确到0.0001)
解 在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:
),按下列顺序依次按键:

显示结果为0.349 215 633.
所以 cot70゜45′≈0.3492.
(1) 由锐角三角函数值求锐角
例4 已知tan x=0.7410,求锐角x.(精确到1′)
解 在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:
),按下列顺序依次按键:

显示结果为36.538 445 77.
再按键:
显示结果为36゜32′18.4.
所以,x≈36゜32′.
例5 已知cot x=0.1950,求锐角x.(精确到1′)
分析 根据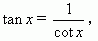 ,可以求出tan x的值,然后根据例4的方法就可
,可以求出tan x的值,然后根据例4的方法就可
以求出锐角x的值.
1.复习回顾,引出新知
课前热身
(参见励耘精品系列丛书《课时导航》华师大版八年级(下)P52“课前热身”)
上面两个题目在做的过程中我们都运用了前一堂课所熟记的特殊角度的三角函数值直接进行解题的,那么下面请同学们来看一下下列题目,你打算怎么解决。
(1)计算sin36°30′= ;cos32°20′= ;
tan70°25′= ;cot13°13′= 。
(2)若sinα=0.8526,那么α的值为多少?
还可以用昨天的方法勾画三角形,然后进行测量计算,但比较麻烦,所以今天我们来借助计算器进行运算。
|
2.画角的平分线,已知直线的垂线和线段的垂直平分线 |
|
|
1.角平分线的尺规画法. 2.过一点画已知直线的垂线 |
3.线段的垂直平分线的尺规画法. |
2.巩固练习
①画个直角三角形,使其直角边分别等于如图所示的两条线段.

②画一个角,使其等于如图所示的∠A.
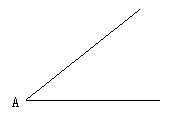
③试把图中所示的角四等分.
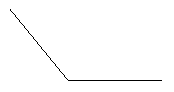
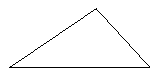
④画一个四边形,使它的面积等于如图所示的三角形的面积的2倍.
[答案] 略
1.链接生活
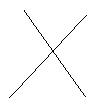
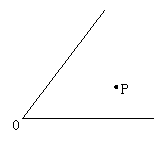
如图所示,要在两条交叉的公路中间的空地上修建一个加油站P,使P到两条公路及它们的交叉点的距离相等,你怎样定出加油站P的位置呢?
5.学习小结
(1)内容总结:
①角平分线的尺规画法;
②过一点画已知直线的垂线;
③线段的垂直平分线的尺规画法.
(2)方法归纳:本节课所学习的三种尺规作图,内容上虽各不相同,但其本质都有很大的联系.如:我们可以把垂线的作图转化为平角的角平分线的作图.
4.达标反馈
(1)如图所示,过点P画∠O两边的垂线.
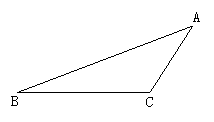
(2)如图所示,画△ABC的BC边上的高.
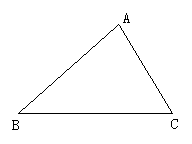
(3)画出图中三角形三个内角的平分线.
[答案] 略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com