
2.提高学生对角平分线性质和判别在实际生活中的应用能力.
1.掌握角的平分线性质定理和判定定理,并能运用这两个定理证明线段相等和角相等.
3.
 (04重庆)如右图,CD是平面镜,光线从A点出发经过CD上点E反射后照射到B点,若入射角为
(04重庆)如右图,CD是平面镜,光线从A点出发经过CD上点E反射后照射到B点,若入射角为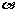 (入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan
(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan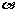 的值为( )
的值为( )
A. 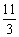 B.
B.
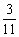 C.
C.
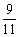 D.
D.
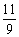
2.
(03汕头)已知∠A是锐角,且tanA、cotA是关于x的一元二次方程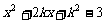 =0的两个实数根.
=0的两个实数根.
(1)求k的值;
(2)问∠A能否等于45°?请说明你的理由.
1. (03新疆)
(1)如图,锐角的正弦值和余弦值都随着锐角的确定而确定、变化而变化. 试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°,这些锐角的正弦值和余弦值的大小.
(3)比较大小(在空格处填“>”、“<”或“=”)
 若
若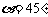 ,则
,则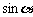 ______
______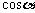 ;若
;若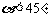 ,则
,则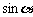 ______
______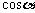 ;若
;若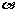 >45°,则
>45°,则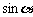 ______
______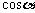 .
.
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:
Sin10°、cos30°、sin50°、cos70°.
2.
 如下图所示,在△ABC中,∠C=90°,D是AC边上一点,且
如下图所示,在△ABC中,∠C=90°,D是AC边上一点,且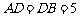 ,
,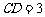 ,求
,求 和
和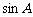 .
.
能力提高练习
1.
(03兰州)计算: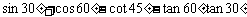 .
.
5.
已知:如图,在△ABC中,∠A=30°,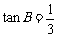 ,
,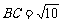 ,则AB的长为______________.
,则AB的长为______________.
4.
 (04沈阳)在Rt△ABC中,∠C=90°,
(04沈阳)在Rt△ABC中,∠C=90°,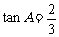 ,AC=4,则BC=_____________.
,AC=4,则BC=_____________.
3.
(03襄阳) =_______________.
=_______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com