
4.人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只,正以24海里/小时的速度向正东方向航行.为迅速实施检查,巡逻艇调整好航向,以26海里/小时的速度追赶,在涉嫌船只不改变航向和航速的前提下,则(1)需要 小时才能追上;(点B为追上时的位置)(2)确定巡逻艇的追赶方向为 度(精确到0.1°).
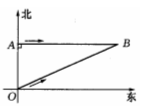
3.今年入夏以来松花江哈尔滨段水位不断下降,达到历史最低水位.一条船在松花江某水段自西向东沿直线航行(如下图),在A处测得航标C在北偏东60°方向上.前进100米到达B处,又测得航标C在北偏东45°方向上,在以航标C为圆心,120米长为半径的圆形区域内有浅滩.如果这条船继续前进,是否有被浅滩阻碍的危险?
2.渔船以32.6海里/时的速度向正北方向航行,在A处看灯塔在渔船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与渔船的距离最短,则灯塔Q到B处的距离为 海里(画出图形后计算,精确到0.1海里).
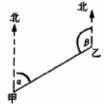
1.如下图所示,甲、乙两地间要修一条公路,从甲地测得公路的走向是北偏东50°,如果甲、乙两地同时开工,要使公路准确接通,在乙地应按∠β为 度施工.
求解与方位角有关的实际问题时,在理解题意后需构造直角三角形(通常作航行方向或施工路线、走向的垂线),用列方程的方法解直角三角形.
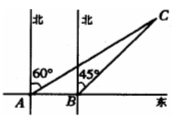
例1 如下图所示,海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里后到达点C处,又测得海岛A位于北偏东30°.如果渔船不改变航向继续向东航行,有没有触礁的危险?
分析 欲判断渔船继续向东航行有无触礁危险,需计算出该岛到航线的最近距离比8海里大还是小.为此,作AD⊥BC,交BC延长线于D.要求AD,必须解直角三角形.图中Rt△ABD和Rt△ACD分别有30°和60°的角;可设公共边AD= x,则CD=AD·cot60°,BD=AD·cot30°,再利用BD-CD=BC即可求出x.

答 若渔船不改变航向继续向东航行,与海岛A的距离最小时大于8海里,没有触礁的危险.
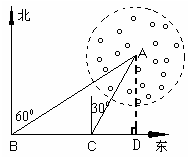
例2 上午10时正,某渔轮在小岛O北偏东30°方向、距离10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.求渔轮何时到达小岛O的正东方向?(精确到1分钟)
分析 学生虽然在初一接触过方向角,但应用很少,所以在解决这个问题时,可能出现不会画图、无法将实际问题转化为数学问题的情况.因此教师在学生独自尝试之后应加以引导:(1)确定小岛O点;(2)画出10点时船的位置A;(3)小船在A点向南偏东60°航行,到达O的正东方向位置在哪?设为B;(4)结合图形引导学生加以分析,可以解决这一问题.
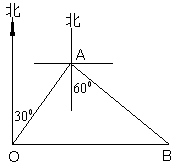
答 船到达点B的时刻为11时44分.
如下图所示,海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,请同学们考虑:如果渔船不改变航向继续向东航行.怎样判断渔船是否有触礁的危险?
我们要确定是否有危险的话,就必需想办法预先求出渔船在航行过程中距离海岛的最近距离是多少,如果大于8海里则是安全的,否则不安全.在这个实际问题中,我们就需要应用方位角和解直角三角形的有关知识.下面我们通过具体的例题来看此类问题的解决方法.
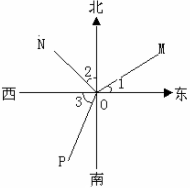
在下图中,∠1=30°,∠2=45°,∠3=60°,则射线OM的方位角是___________, ON的方位角是 ___________,OP的方位角是 ___________.
7、巩固练习:课本第19.4中第2、3题和第120页复习题中第10题第121页中第14题。
[板书设计]
|
19.4解直角三角形 仰角是视线方向向水平线上方,这时视线与水平线的夹角. 俯角是视线向水平线下方,这时视线与水平线的夹角. 梯形通常分解成矩形和直角三角形(或分解成平 行四边形与直角三角形). |
投影 |
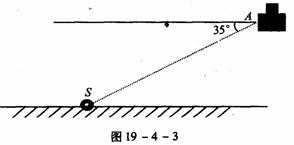
6、实践活动:如图19-4-3所示,一飞机在1500米的高空中测得地面控制塔的俯角为 ,求这时收音机距指挥塔的直线距离是多少米?
,求这时收音机距指挥塔的直线距离是多少米?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com