2．写出下列命题的逆命题，并判断这些命题的真假．

(1)如果∠α与∠β是邻补角，那么∠α+∠β=180°；

(2)如果一个三角形的两个内角相等，那么这两个内角所对的边相等．

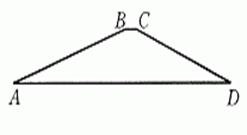
1．在两个直角三角形中，有两条边分别对应相等，这两个直角三角形一定全等吗？如果不一定全等，请举出一个反例．

　 参见励耘精品系列丛书《课时导航》华师大版八年级(下)P55－P56

⒈解直角三角形应用题的基本思路：从图形中找出含已知和所求的边、角的直角三角形，把问题转化为解某个直角三角形。

⒉锥度的相关概念及关系式。

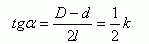
⒊坡度的相关概念及关系。

指出上述概念是我们解题的工具必须熟记。

2．已知铁路路基横断面为一等腰梯形，腰的坡度为2：3，路基高为3m，底宽为12m，则路基顶宽为多少？　

(此题改编自励耘精品系列丛书《课时导航》华师大版八年级(下)P56第14题)

1．一水库大坝的横断面为梯形ABCD，坝顶宽6.2米，坝高23.5米，斜坡AB的坡度i₁＝1∶3，斜坡CD的坡度i₂=1∶2.5.求：

(1)斜坡AB与坝底AD的长度；(精确到0.1米)

(2)斜坡CD的坡角α.(精确到1°)

0.1米)

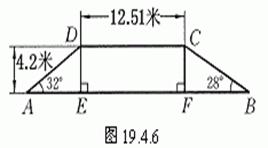
答： 路基下底的宽约为27.13米．

2.坡度的概念。

在修路、挖河、开渠和筑坝时，设计图纸上都要注明斜坡的倾斜程度.

如图19.4.5，坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比).记作i,即i=h/l.

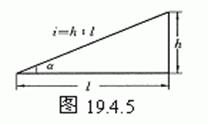
坡度通常写成1∶m的形式，如i=1∶6.

坡面与水平面的夹角叫做坡角，记作a，有

显然，坡度越大，坡角a就越大，坡面就越陡.

例2　如图19.4.6，一段路基的横断面是梯形，高为4.2米，上底的宽是12.51米，路基的坡面与地面的倾角分别是32°和28°．求路基下底的宽．(精确到

1.锥度的概念

例1　 一锥形零件轴截面如图，图纸上规定锥度k是1：8，求斜角α。

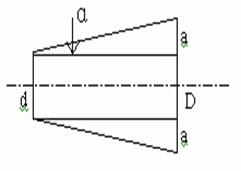
讲解注意以下几点：

⑴讲清锥度的概念，，指出机械加工中所指的锥形包括圆锥和圆台形，课本是用“大头直径D与小头直径d的差与锥形部分长度的比”来定义锥度，并用字母来表示，即

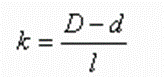
对于圆锥形可理解为小头直径为零，所以

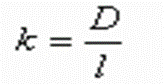
但是，在机械加工中遇到的多数是圆台形的零件。

⑵锥形零件中斜角的概念。结合图5-13说明，指出利用解直角三角形，可以得到斜角α与锥度k的关系。

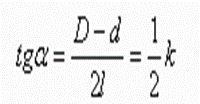
搞清这一关系，就能顺利地进行有关锥度的计算，可以求D，d，l，k，α中任何一个量。

⒈什么叫解直角三角形？

⒉解直角三角形有着广泛的应用，本次课我们通过举例来说明。(板书课题)