3． 角平分线

教学目的：角平分线定理及逆命题的应用

重点与难点：角平分线定理及逆命题的应用

教学过程：

回 忆

我们知道角平分线上的点到这个角的两边的距离相等．角平分线的这条性质是怎样得到的呢？

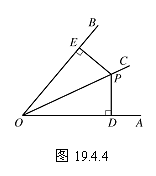
如图19．4．4，OC是∠AOB的平分线，点P是OC上任意一点，PD⊥OA， PE⊥OB，垂足分别为点D和点E．当时是在半透明纸上描出了这个图，然后沿着射线OC对折，通过观察，线段PD和PE完全重合．于是得到PD＝PE．

与等腰三角形的判定方法相类似，我们也可用逻辑推理的方法加以证明.图中有两个直角三角形△PDO和△PEO，只要证明这两个三角形全等，便可证得PD＝PE．

于是就有定理：

角平分线上的点到这个角的两边的距离相等．

此定理的逆命题是“到一个角的两边的距离相等的点在这个角的平分线上”，这个命题是否是真命题呢？即到一个角的两边的距离相等的点是否一定在这个角的平分线上呢？我们可以通过“证明”来解答这个问题．

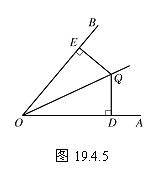
已知： 如图19．4．5，QD⊥OA， QE⊥OB，点D、E为垂足，QD＝QE．

求证： 点Q在∠AOB的平分线上．

分析： 为了证明点Q在∠AOB的平分线上，

可以作射线OQ，然后证明Rt△DOQ≌Rt△EOQ，从而得到∠AOQ＝∠BOQ．

于是就有定理：

到一个角的两边距离相等的点，在这个角的平分线上．

上述两条定理互为逆定理，根据上述这两条定理，我们很容易证明： 三角形三条角平分线交于一点．

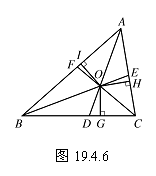
从图19．4．6中可以看出，要证明三条角平分线交于一点，只需证明其中的两条角平分线的交点一定在第三条角平分线上就可以了．

请你完成证明．

课堂练习：

4． 给定一个三角形的两边长分别为5、12，当第三条边为多长时，这个三角形是直角三角形？

课堂小结：总结一下你所学过的知识

3． 三角形三边长a、b、c分别是下列各组数，试判断各三角形是不是直角三角形？如果是，那么哪一个角是直角？

(1) a=8, b=15, c=17；(2) a=6, b=10, c=8；

(3) a=1, b=3, c=2.

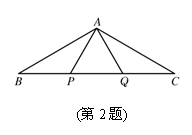
2． 如图，已知P、Q是△ABC的边BC上两点，并且BP＝PQ＝QC＝AP＝AQ，求∠BAC的大小．

1． 说出定理“等边三角形的三个内角都相等”的逆命题，并证明该逆命题为真命题．

2. 理解并能用勾股定理的逆定理

重点与难点：本节两个定理的应用

教学过程：

在七年级第二学期第10章中我们已经知道，等腰三角形的底角相等，这是等腰三角形的性质定理．它的逆命题“如果一个三角形有两个角相等，那么这两个角所对的边也相等”也是定理，是判定三角形是否是等腰三角形的一个重要的方法．

回 忆

你是怎样知道等腰三角形的这个判别方法的呢？

如图19．4．1，在△ABC中，∠B＝∠C．当时是利用圆规截取AB、AC，比较AB、AC的大小，从而得到AB＝AC．

为了确认这个命题的正确性，我们可以用逻辑推理的方法加以证明．

已知： 如图19．4．2，在△ABC中，∠B＝∠C．

求证： AB＝AC．

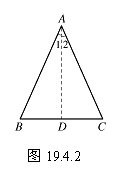分析： 要证明AB＝AC，可设法构造两个全等三角形，使AB、AC分别是这两个全等三角形的对应边，于是想到作∠BAC的平分线AD．

证明　　　　 作∠BAC的平分线AD．

在△BAD和△CAD中，

∵ ∠B＝∠C，

∠1＝∠2，

AD＝AD，

∴ △BAD≌△CAD(A．A．S．)，

∴ AB＝AC(全等三角形的对应边相等)．

于是得到：

如果一个三角形有两个角相等，那么这两个角所对的边也相等．(简写成“等角对等边”)

在八年级上学期第14章中我们已经知道勾股定理及勾股定理的逆定理．我们也可以用逻辑推理的方法证明勾股定理的逆定理．

如果三角形的一条边的平方等于另外两条边的平方和，那么这个三角形是直角三角形．

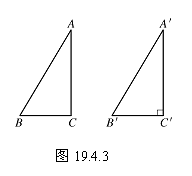
已知： 如图19．4．3，在△ABC中，AB＝c， BC＝a， CA＝b，且a2+b2＝c2．

求证： △ABC是直角三角形．

分析： 首先构造直角三角形A′B′C′，使∠C′＝90°，B′C′＝a， C′A′＝b，然后可以证明△ABC≌△A′B′C′，从而可知△ABC是直角三角形．

设三角形三边长分别是下列各组数，试判断各三角形是不是直角三角形．如果是直角三角形，请指出哪条边所对的角是直角．

(1) 7， 24， 25；(2) 12， 35， 37；(3) 35， 91， 84．

课堂练习：

2． 等腰三角形的判定

教学目的：1. 理解并能用等腰三角形的等角对等边

3． 在你所学过的知识内容中，有没有原命题与逆命题都正确的例子(即互逆定理)？试举出几对．

课堂小结：总结一下你所学过的知识

作业：P94.1

2． 举例说明下列命题的逆命题是假命题：

(1) 如果一个整数的个位数字是5，那么这个整数能被5整除；

(2) 如果两个角都是直角，那么这两个角相等．

1． 说出下列命题的题设和结论，并说出它们的逆命题：

(1) 如果一个三角形是直角三角形，那么它的两个锐角互余；

(2) 等边三角形的每个角都等于60°；

(3) 全等三角形的对应角相等；

(4) 到一个角的两边距离相等的点，在这个角的平分线上；

(5) 线段的垂直平分线上的点到这条线段的两个端点的距离相等．