4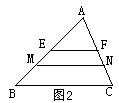． 如图，△ABC中，EF是它的中位线，M、N分别是EB、CF的

中点，若BC=8cm，那么EF=　　　　 cm，MN=　　　　 cm；

3．若边长为4cm的菱形的两邻角度数之比为1∶2，则该菱形的面积为　　 　cm²。

2．平行四边形ABCD的周长为20cm，对角线AC、BD相交于点O，若△BOC的周长比△AOB的周长大2cm，则CD＝　　　 cm。

1．平行四边形ABCD中，∠A=50⁰，AB=30cm，则∠B=____，DC=____ cm。

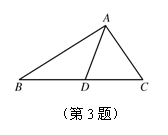
3． 如图，在△ABC上，已知点D在BC上，且BD+AD＝BC．求证： 点D在AC的垂直平分线上．

课堂小结：总结一下你所学过的知识

作业：P94.　 5，6

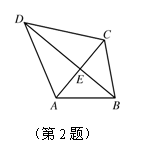
2． 如图，已知AE＝CE， BD⊥AC．求证： AB+CD＝AD+BC．

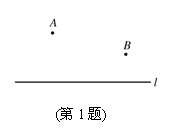
1． 如图，已知点A、点B以及直线l，在直线l上求作一点P，使PA＝PB．

4． 线段垂直平分线

教学目的：线段的垂直平分线定理及逆定理

重点与难点：线段的垂直平分线定理及逆定理的应用

教学过程：

我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴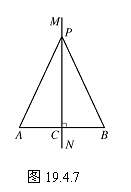，并知道线段的垂直平分线上的点到这条线段的两个端点的距离相等．我们也可用逻辑推理的方法证明这一结论．

如图19．4．7，设直线MN是线段AB的垂直平分线，点C是垂足．点P是直线MN上任意一点，连结PA、PB．证明PA＝PB．

已知： MN⊥AB，垂足为点C，AC＝BC，点P是直线MN上任意一点．

求证： PA＝PB．

分析　　 图中有两个直角三角形APC和BPC，只要证明这两个三角形全等，便可证得PA＝PB．

于是就有定理：

线段的垂直平分线上的点到这条线段的两个端点的距离相等．

此定理的逆命题是“到一条线段的两个端点的距离相等的点在这条线段的垂直平分线上”，这个命题是否是真命题呢？即到一条线段的两个端点的距离相等的点是否一定在这条线段的垂直平分线上呢？我们也可以通过“证明”来解答这个问题．

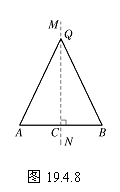已知： 如图19．4．8，QA＝QB．

求证： 点Q在线段AB的垂直平分线上．

分析： 为了证明点Q在线段AB的垂直平分线上，可以先经过点Q作线段AB的垂线，然后证明该垂线平分线段AB；也可以先平分线段AB，设线段AB的中点为点C，然后证明QC垂直于线段AB．

于是就有定理：

到一条线段的两个端点的距离相等的点，在这条线段的垂直平分线上．

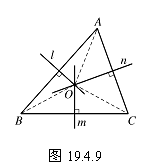上述两条定理互为逆定理，根据上述两条定理，我们很容易证明： 三角形三边的垂直平分线交于一点．

从图19．4．9中可以看出，要证明三条垂直平分线交于一点，只需证明其中的两条垂直平分线的交点一定在第三条垂直平分线上就可以了．

试试看，现在你会证了吗？

课堂练习

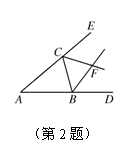
2． 如图，已知△ABC的外角∠CBD和∠BCE的平分线相交于点F，求证： 点F在∠DAE的平分线上．

课堂小结：总结一下你所学过的知识

作业：P94。4

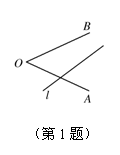
1． 如图，在直线l上找出一点P，使得点P到∠AOB的两边OA、OB的距离相等．