
2.课前热身
互动1
师:请同学们思考一下,他这样测行吗?有什么依据吗?
生:他这样测可以.因为由三角形的一个外角等于两个不相邻的两个内角和可以求出∠B=30°,又因为∠B=∠C,所以AB=AC.
师:很好.军军这种方法其实就是利用“等角对等边”,那么同学们是怎样知识等腰三角形的这个识别方法的呢?
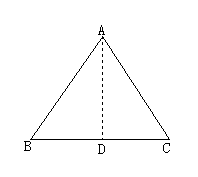 生:用折纸的方法.如图所示,△ABC中,∠B=∠C,利用刻度尺找到BC的中点D,连结AD,然后沿AD对折,观察发现AB、AC完全重合,于是得到AB=AC.
生:用折纸的方法.如图所示,△ABC中,∠B=∠C,利用刻度尺找到BC的中点D,连结AD,然后沿AD对折,观察发现AB、AC完全重合,于是得到AB=AC.
明确 回顾在第9章得出的“等角对等边”这个识别等腰三角形的重要方法.
1.情境导入
军军想利用学过的知识测一测河宽(如图所示).他先沿着垂直于河岸的方向在河两岸分别选定两点A、B,再从A点到C点,测得∠C=30°,∠DAC=60°,量一量AC的长度就是河宽.

2.经历探索证明方法的过程,逐步培养学生逻辑推理的能力.
1.掌握等腰三角形的判定定理、性质定理以及斜边、直角边定理的证明.
2. 将对本课题的探究体验写成一个学习报告,与同学交流..
活动与探究
如果我们身旁没有量角器或三角尺,又需要做60°、30°、15°等大小的角,可以采用下面的方法(如下图).
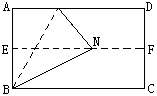
(1)对折矩形纸片ABCD,使AD与BC重和,得到折痕EF,把纸片展平.
(2)再一次折叠纸片,使点A落在EF上,并使折痕过点B,得到折痕BM,同时得到了线段BN.
观察所得的∠ABM、∠MBN和∠NBC,在三个角有什么关系?你能证明吗?
通过证明可知,简单而准确.由此,15°、60°、120°、150°等角,就都容易得到了.
已知:矩形ABCD,E、F分别为边AB、CD的中点,N在EF上,且MN=AM,(如图),BN=AB.
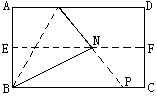 求;∠ABM、∠MBN和∠NBC的大小
求;∠ABM、∠MBN和∠NBC的大小
解:如右图延长MN交BC于点P
∵AM=MN,AB=NB,BM=BM,
∴△ABM≌△NBM(SSS)∴∠ABM=∠MBN.
又∵EF为矩形ABCD的中位线,
∴MN=NP.
又∵BN=BN,∠BNM=∠BNP=Rt∠.
∴△BMN≌△BPN.
∴∠MBN=∠NBP.
∴∠ABM=∠MBN=∠NBP=30°.
1. 复习总结两节课的探究结论,并作进一步的思考与认识.
在前一节课的探索基础上,我们进一步对、任意多边形等一些不规则几何图形的重心进行了探究.在实际操作过程中,同学们充分发挥自己的主动性,积极思考、大胆设想,体现了我们探究性学习的主旨,可以说,我们在这节课中收获是很大的.
3. 在另一个小钉上重复(2)的活动,找到两条铅垂线的交点.
上面的操作同学们都完成了吧?下面我们先来思考一个问题:如果在第三个小钉上重复上述活动中的(2),那么第三铅垂线会经过前两条铅垂线的交点吗?
同学们想得很正确,这一点确实是这个三角板的重心.前面的学习中我们就知道,用手指顶住物体的重心位置,物体会保持平衡.同样的道理,将物体悬挂后,物体保持平衡时,说明物体所受的力处于平衡状态,即每次所保留下来的铅垂线都要经过薄板的重心,那么两条铅垂线的交点就理所当然是薄板的重心了.
对于一个任意的三角形来说,我们要找它的重心,不可能每次都把它做成薄板去悬挂,所以我们有必要对上面操作的结果做进一步的分析,得到三角形重心的确切位置.
同学们找一下三条铅垂线与三角形三边的交点,看看交点的位置.
这三条铅垂线与对边的交点好像是对边的中点.
同学们想办法来证明一下,看是不是边的中点.
用刻度尺量一量,确实是三角形边上的中点.
我们数学还要有充分的理论依据,请大家认真思考,可以采用逆向思维:如果是中点,会有什么结果,也就是找找该点为边的中点的理论依据.
(思考、讨论)我觉得三角形薄板悬挂后,薄板处于平衡状态,那么说明铅垂线两侧的两部分一样重.这个薄板很均匀,使用我觉得铅垂线是将三角形薄板分成面积相等的两部分了,根据三角形面积公式,只能是所分得的两个小三角形的底边相等,所以说铅垂线肯定过了对边的中点.
这位同学分析得太精彩了,有理有据,思路条理、清楚,这说明三角形的重心是三条中线的交点.(播放课件)
结论:三角形的三条中线交于一点.这一点就是三角形的重心.
不同形状、不同类型的三角形的重心又会有什么不同?它们是否都在三角形内部?如下图所示.
第一组:我们组是找的锐角三角形的重心,它就在三角形内部.(如图a)
第二组:我们的研究的直角三角形,我们发现直角三角形的重心也在三角形内部(如图b)
第三组:我们研究的是钝角三角形,钝角三角形,钝角三角形的重心仍在三角形上,而且在三角形的内部.
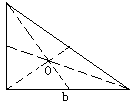
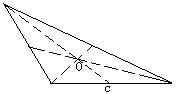
 很好可以看出,三角形的重心全在三角形的内部,并且是三条中线的交点.
很好可以看出,三角形的重心全在三角形的内部,并且是三条中线的交点.
有了上面的内容做依据,我们可以很轻松地来完成下面的探究:
探究四:任意多边形的重心.
活动过程:
将任意多边形的薄板分发给每组同学,由学生仿照探究三中的方法,找到任意多边形的重心.
如图为任意五边形的重心.
在探究的过程中我们发现正五边形,正六边形等图形的重心也是它们的中心.
这样我们就可以得出这样的结论:规则几何图形的重心就是该图形的几何中心,而不规则的几何图形的重心需通过悬挂法来找.同学们请看大屏幕(播放课件).
课题总结:
通过这个课题学习活动,可以得出如下结论:
(1) 对于线段、平行四边形、等边三角形、正五边形、正六边形等规则的几何图形,它们的重心就是该图形的几何中心.
(2) 对于任何的多边形这些不规则的几何图形,它们的重心就需要采用悬挂法来找.
在得到这些结论的过程中,同学们能够互相配合,充分发挥自己的才智,积极主动地参与到我们的探索中来,我相信每个同学对这两节课探究都会有很深切的体会.
2. 用下端系有小重物的细线缠绕在一个小钉上,吊起薄板,记下铅垂线的“痕迹”;
我们这一节内容,和物理之间有着很密切的联系.在物理学的力学部分有一个很重要的力,叫做重力.重力很重要,可以说离开重力,我们的世界就没有了规则,没有了界限,就会一片混乱.而重力的着力点就叫做物体的重心.
我们在这儿介绍这个力,就是引导同学们试着从力学的角度入手,来探究一些不规则几何图形的重心.
探究三: 三角形的重心.
活动过程:
先分组,然后各种对不同形状的三角形进行研究.
1. 在三角形薄板的每个顶点处钉一个小钉作为悬挂点;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com