4．达标反馈

(1)如图所示，△ABC中，D在BC上，BC=12，BD+AD=12，则点D在　 AC　 的垂直平分线上．

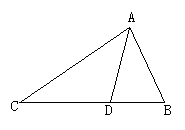
(2)如图，在△ABC中，AB的垂直平分线交AC于D，若AC=8，CB=6，则△BDC的周长是　 14　 ．

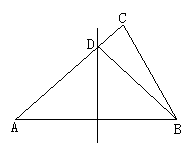
　　 (3)若一个三角形的两边的垂直平分线的交点在第三边上，则这个三角形是　 直角三角形　 ．

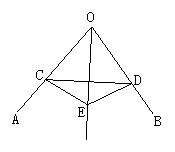
(4)如图所示，OE平分∠AOB，EC⊥OA于C，ED⊥OB于D，求证：a．OC=OD；b．OE垂直平分CD．(提示：利用角平分线性质定理及“H．L”定理证明△OCE≌△ODE)

3．合作探究

　　 (1)整体感知

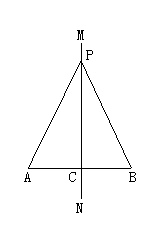请同学们先将这个命题画出图形(如图所示)，写出已知、求证．

　　 (2)四边互动

　　 互动1

　　 师：这又是证明线段相等的命题，回忆上节课证明角平分线性质定理的方法，会得到什么启发？

　　 生：可以利用S．A．S．定理证明△PAC≌△PBC，从而得到PA=PB．

　　 师：很好．这样就得到了线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端点距离相等．

　　 今后我们可以直接利用这个定理直接得到有关线段相等，同时这也可当作等腰三角形的一种判定方法．

　　 明确　 巩固利用三角形全等来证明线段相等的方法．

　　 互动2

　　 师：反过来，到一条线段的两个端点的距离相等的点是否一定在这条线段的垂直平分线上呢？我们也可以通过“证明”来解决这个问题．

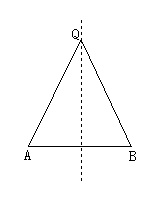
生：画出图形(如图所示)，写出已知，求证．

　　 师：为了证明Q点在AB的垂直平分线上，可以过Q作辅助线，先构造“垂直或平分”中的一个关系，去证明另一个．特别要注意防止“过Q作线段AB的垂直平分线”这种错误．你能根据提示，说出证明过程吗？

　　 生：(略)

　　 师：在证明过程中，很巧妙地利用了前面学习过的等腰三角形“三线合一”的性质，看来同学们能够学以致用，这一点很好．这样我们又得到了线段垂直平分线的判定定理：到一条线段两端点距离相等的点，在这条线段的垂直平分线上．

　　 生：判定定理只能判断点在线段垂直平分线上，那怎么才能判断这条直线就是线段的垂直平分线呢？

　　 师：这个问题提得很好．大家想一想，几点确定一条直线？

　　 生：两点．

　　 师：所以，只要我们能证明一条直线上有两点满足判定定理的条件，那么这条直线就一定是线段的垂直平分线．

　 　明确　 利用等腰三角形“三线合一”证明的方法值得重视．

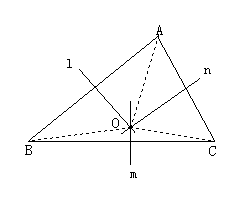例：已知：如图所示，△ABC中，m，n，L分别是BC、AC、AB边上的垂直平分线，求证：m，n，L必交于一点．

　　 证明：设m、n交于一点O，连接OA、OB、OC．

　　 则有OA=OB=OC(线段垂直平分线上的点到线段两端的距离相等)

　　 因为OA=OB

　　 所以O在L上(到线段两端距离相等的点在线段的垂直平分线上)

　　 即m、n、L交于一点

　 　明确　 巩固证明“三线共点”的方法．

　　 师：这道例题的结论又告诉我们，三角形的三条边的垂直平分线也交于一点，这一点称为三角形的外心，外心的性质是到三角形的三个顶点的距离相等．

2．课前热身

　　 利用三角板、刻度尺作出线段a的垂直平分线，在垂直平分线上取点，连结可得符合条件的等腰三角形．

　　 在这里，我们利用了线段垂直平分线上的点到线段两个端点的距离相等．

　　 那么，这条性质又怎么证明呢？下面我们一起来研究．

1．情境导入

给一条已知线段a(如图所示)，以a为底边的等腰三角形有几个？如果用三角板和刻度尺，你能画出至少三个吗？

2．在数学认识发展要求上，让学生掌握线段垂直平分线的性质定理、判定定理的证明，弄清它们的区别与联系，并且会加以应用．

　　 (二)教学过程

1．通过面向真实世界问题设计，强化现实世界是问题源泉的理念．

　　 (1)链接生活

　　 通过这节课的学习，请你设计一种方案，测出操场上旗杆的高度．

　　 (2)巩固练习

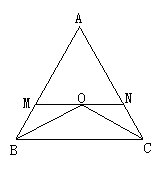
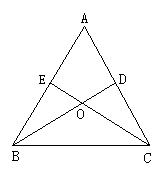
①如图所示，在△ABC中，∠ABC=∠ACB，∠ABC与∠ACB的平分线交于点O，过O作MN∥BC交AB于M，交AC于N，则图中共有 　5　 个等腰三角形．

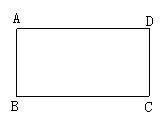
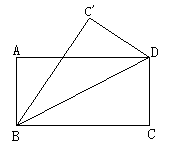
②将一张矩形纸片ABCD沿对角线对折(如图所示)，求证：重叠部分是一个等腰三角形．(提示：利用矩形对边平行的性质及折叠过程中的全等三角形证明)

　　 (四)板书设计

5．学习小结

　　 (1)引导学生作知识总结，通过本节课的学习掌握了等腰三角形的判定定理、性质定理的证明，同时还得出“三线合一”这一重要性质，并且利用等腰三角形性质定理证明了“H．L”定理．

　　 (2)教师扩展：今天学习的几条定理是今后证明两条线段相等、两个角相等及两条直线互相垂直的重要依据．

4．达标反馈

　　 (1)填空

　　 ①根据等腰三角形三线合一的性质，在△ABC中，

　　 (a)∵AB=AC，AD⊥BC，∴∠BAD=∠CAD，BD=CD．

　　 (b)∵AB=AC，AD是中线，∴∠BAD=∠CAD，AD⊥BC．

　　 (c)∵AB=AC，AD是角平分线，∴AD⊥BC，BD=CD．

　　 ②等边三角形各角都 　相等 　，且每一个角都等于　 60° 　．

　　 ③等腰直角三角形的每个锐角为　 45° 　，斜边上的高把直角分成的两个锐角为　 45° 　．

　　 ④三角形中，若有两个角的平分线都垂直于对边，则此三角形是　 等边 　三角形．

　　 (2)证明：

　　 ①等腰三角形顶角的外角平分线与底边平行．

　　 ②如图所示，△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE交于O点．

　　 求证：1°△BCD≌△CBE；2°△BOE≌△COD．

　　 [答案]　 (略)