3.　　　　 (03鄂州)△ABC中，∠C=90°，点D在BC上，BD=6，AD=BC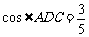，，则DC的长为____________.

2.　　　　 (04绍兴)如图，河对岸有古塔AB，小敏在C处测得塔顶A的仰角为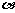，向塔前进s米到达D，在D处测得A的仰角为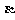，则塔高是_________米.

1.　　　　 (03绍兴)若某人沿坡度为3∶4的斜坡前进10m，则他所在的位置比原来的位置升高___________m.

4.　　　　 (04金华)在Rt△ABC中，∠C=90°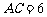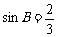，，，那么AB的长是(　　 )

A. 4　　　　　　　　　　　　　　 B. 9　　　　　　　　　　　　　　 C. 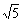　　　　　　　　　　　　 D.

3.　　　　 (03孝感)铁路路基的横断面为等腰梯形，其腰的坡度为2∶3，顶宽6米，路基高4米，则路基的下底宽为(　　 )

A. 18米　　　　　　　　　　　 B. 15米　　　　　　　　　　　 C. 12米　　　　　　　　　　　 D. 10米

2.　　　　 (03恩施)如右图，测量人员在山脚A处测得山顶B的仰角为45°，沿着仰角为30°的山坡前进1000米到达D处，在D处测得山顶B的仰角为60°，则山高BC大约是(精确到0.01米)(　　 )

A. 1366.03米　　　　　　　　　　　 B. 1482.12米

C. 1295.93米　　　　　　　　　　　 D. 1508.21米

1.　　　　 (03黄石)每周一学校都要举行庄严的升国旗仪式，让我们体会到了国旗的神圣. 某同学产生了用所学知识测量国旗杆高度的想法. 在地面距杆脚5m远的地方，他用测倾仪测得杆顶的仰角为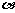，且，则杆高(不计测倾仪高度)为(　　 )

A. 10m　　　　　　　　　　　　　　　　 B. 12m

C. 15m　　　　　　　　　　　　　　　　 D. 20m

2．巩固练习

(1)如图所示，已知直线L和L外两点A和B，在L上求作一点P，使PA+PB最小．

(2)如图所示，△ABC中，AD为∠A的平分线，FE垂直平分AD，E为垂足，交BC的延长线于F，求证：∠B=∠CAF．

(提示：∠B=∠ADF-∠BAD，∠CAF=∠DAF-∠DAC ，又∠ADF=∠DAF，∠BAD=∠DAC)

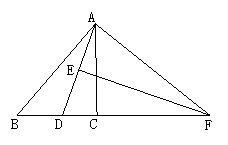
(3)如图所示，△ABC中，AD⊥BC于D，AB+BD=DC，求证：∠B=2∠C．

(提示：在DC上截取DE=DB，连结AE，证明AE=AB从而CE=AE，所示∠AED=2∠C)

1．链接一：在城区有三所小学A、B、C，现准备修建一座儿童游乐中心P，应修在何处，才能使三所小学到游乐中心的距离相等．

　　 链接二：在公路的同侧有两个工厂，为了便于两厂的工人看病，市政府计划在公路边修建一所医院，使得两个工厂的工人都没有意见，问医院的院址应选在何处？

5．学习小结

　　 (1)引导学生作知识总结：线段垂直平分线的性质、判定定理、三角形的外心及作法和性质．

　　 (2)教师扩展：利用两个定理证明线段相等，线段垂直时不用再证明全等，可简化解题过程．