
能熟练地解直角三角形,会把矩形、梯形、非直角三角形的图形进行分解化归为直角三角形问题。
2、要学会将千变万化的实际问题转化为数学问题来解决的能力,要求学生善于将某些实际问题中的数量关系归结为直角三角形中元素之间的关系,培养学生用数学的意识。
1、学会用解直角三角形的有关知识去解决某些简单的实际问题(包括一些能用直角三角形解的斜三角形问题),从而进一步把形和数结合起来,提高学生分析问题和解决问题的能力;
3.
解:∵AB=2米,tan∠ACB=2∶1,∴BC=1米,∴ .
.
∵550米长的坡平均分成了11块,∴每块坡面长为50米. 为减少投资,应用6块坡面种花,5块坡面种草.
∴公路局要将这块坡地美化,最少需要投资
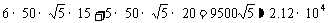 (元).
(元).
2. 解:过点D作DE⊥BC于E,则四边形ACED是矩形. ∴AC=DE,DA=EC=82米,
∠BDE=30°.
在Rt△BDE中,∵ ,∴
,∴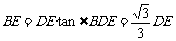 .
.
在Rt△BAC中,∵ ,即
,即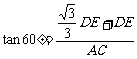 ,
,
∴ =246. 解得
=246. 解得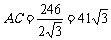 (米)
(米)
∴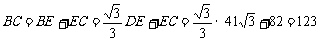 (米).
(米).
答:大厦BC高为123米,小丽所住的电梯公寓与大厦间的距离AC为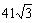 米.
米.
1.
(1)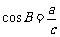 ,c;∠B,∠A+∠B=90°,∠A;a,∠B,
,c;∠B,∠A+∠B=90°,∠A;a,∠B, ,b.
,b.
(2)略.
4.
解;(1)在Rt△ABD中,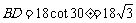 (米).
(米).
(2)设甲楼最高应建x层,有
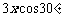 ≤21,即
≤21,即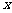 ≤
≤ .
.
取x=4.
∴设甲楼最高应建4层.
能力提高练习
3. 解:如图,作EG⊥FB于G,DH⊥FB于H,记坝高为h,则EG=DH=h.
 由
由 1∶1=1,
1∶1=1,
得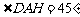 ,
,
∴
= .
.
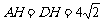 .
.
由 EG∶FG=1∶2,得
EG∶FG=1∶2,得 .
.
∴ .
.
∴海堤断面增加的面积
S梯形FADE=
 (m2).
(m2).
∴工程所需土方=96S梯形FADE≈96×25.0=2400= (m3).
(m3).
答:完成这一工程约需土方 m3.
m3.
2. (1)证明:在Rt△ABD和Rt△ADC中,
∵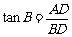 ,
,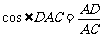 ,又
,又 ,
,
∴ . ∴AC=BD.
. ∴AC=BD.
(2)解:在Rt△ADC中,由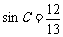 ,可设
,可设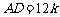 ,则
,则 .
.
由勾股定理,得CD=5k.
又由(1)知BD=AC=13k,∴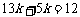 . 解得
. 解得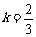 .
.
∴AD=8.
1. 解:Rt△ABC中,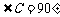 ,
,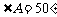 ,∴
,∴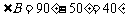 .
.
∵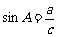 ,∴c=3.
,∴c=3.
∴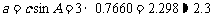 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com