
3、已知直角梯形的一腰长为6cm,这腰与底所成的角为30°,那么另一腰长是( )
2、等腰梯形的上底、高、下底之比为1︰1︰3,则底角的度数为( )
(A)30°(B)45°(C)60°(D)不能确定
1、下列命题中正确的是( )
(A)梯形的两条对角线相等
(B)等腰梯形可能是直角梯形
(C)直角梯形中可以有两边相等
(D)梯形的两个底角相等
(四)作业:B册习题P.35-36 15-20
(三)小结
1、解直角三角形的应用就是把生产生活中的实际问题转化为直角三角形边角间的关系,从而通过解直角三角形来解决,同时培养应用数学的思想意识。
2、对于某些非直角三角形的问题,通过引高构造出直角三角形,从而转化为解直角三角形的问题来解决,即是构造法的具体体现,也是转化思想方法的运用。
(三)旗杆竖在房屋的屋顶上:
工具:测角仪、卷尺;
方法:在地面D处测得旗杆顶A的仰角为α,测得旗杆底B的仰角为β,已知房高为h,测角仪高为b。
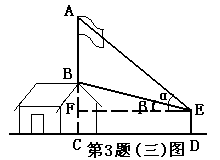
解:设BD=x,由题意得∠AEF=α,∠BEF=β,BC=h,CF=b,在Rt△BEF中,
ctgβ=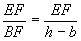 ,∴EF=(h-b)·ctgβ。在Rt△AEF中,
,∴EF=(h-b)·ctgβ。在Rt△AEF中,
tgα=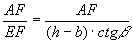 ,∴AF=(h-b)·ctgβ·tgα,∴AB=AF-BF,
,∴AF=(h-b)·ctgβ·tgα,∴AB=AF-BF,
∴AB=(h-b)(ctgβtgα-1)。
4、思考题:
将水库拦水坝背水坡坝顶加宽2米,坡度由原来的1:2改为1:2.5,已知:坝高6米,坝长50米。求加宽部分横断面AEFB的面积;计算完成这一工程需要多少土方?
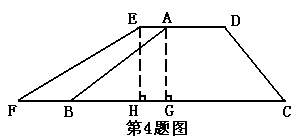
解:过A点、E点作AG⊥BC,EH⊥BC,垂足分别为G、H点,由题意知
AG=EH=6米,AE=HG=2米,在Rt△ABG中,i=1:2,即AG:BG=1:2,得BG=12米,在Rt△EFH中,i=1:2.5,即EH:FH=1:2.5,得FH=15米,∴FB=FH+HG-BG=17-12=5米,
∴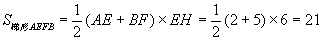 米2,
米2,
∴完成这一工程需要的土方数=50×21=1050米3。
答:梯形AEFB的面积是21平方米。完成这一工程需要土方1050立方米。
(二)旗杆前有一湖(或障碍物),人只能在湖(或障碍物)的另一边进行测量:
工具:测角仪、卷尺;
方法:用测角仪在c点测得旗杆顶点A的仰角为α,在BC的延长线上向后退到D点,测得A点的仰角为β,并用卷尺测得测角仪高为b。
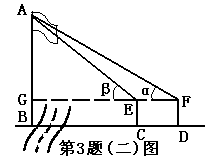
解:在Rt△AEG中、设AG=x,∠AEG=α,∴ctg∠AEG=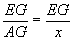 ,
,
∴EG=x·ctgα。同理,在Rt△AFG中,FG=x·ctgβ,∵CD=a,∴FG-EG=a,
∴x=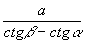 ,∴旗杆AB=x+b=
,∴旗杆AB=x+b=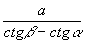 +b。
+b。
(一)旗杆的底部到达地面时:工具:测角仪、卷尺;
方法:用测角仪测量出旗杆顶点A的仰角α,然后用卷尺量出BC之间的距离a,已知测角仪高为b。
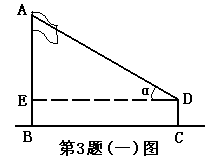
解:在Rt△ADE中,DE=a,∠ADE=α,∴tg∠ADE=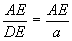 ,∴AE=a·tgα,
,∴AE=a·tgα,
∴旗杆AB=AE+EB=a·tgα+b。
(二)新课:
1、填空
(1)△ABC中,AB=AC=5,BC=6,则tg∠B=________。
(2)某斜面坡度为i=1:0.75,l=4,则h=________。
(3)如图,矩形ABCD的周长为17cm,对角线BD与边CD的夹角的正弦值为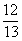 ,则较短边为________。
,则较短边为________。
(4)如图,海面上以灯塔P为中心的15海里的范围内有暗礁,一货轮在海面上A处,测得灯塔P在北偏东60°,相距32海里,如果轮船向正东航行,有没有触礁危险?(______)
(5)如图,旗杆AB,升旗用绳子AC拉直后与地面成60°角,已知绳子比旗杆长1米,则旗杆高________。
2、计算:直角梯形ABCD中,AD∥BC,∠D=90°,∠B=45°,∠ACB=30°。
①设BC为a,求CD;
②若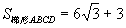 ,求CD。
,求CD。
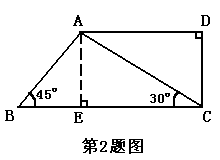
解:过A点作AE⊥BC于E点,
①设CD=x,则AE=x,在Rt△ABE中,∠B=45°,AE=BE=x,
在Rt△ACE中,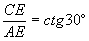 ,∴CE=
,∴CE=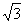 x。∵BE+CE=BC,∴
x。∵BE+CE=BC,∴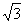 x+x=a,
x+x=a,
∴x=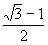 a,∴CD=
a,∴CD=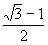 a。
a。
②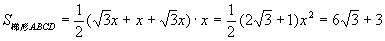 ,∴x=
,∴x=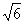 ,
,
∴CD=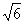 。
。
3、请设计一种测量旗杆高度的方案
(一)知识回顾:
1、在Rt△ABC中,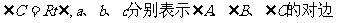
⑴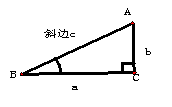 角的关系:___________________
角的关系:___________________
⑵边的关系:___________________

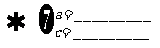
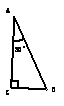

直角边等于斜边的一半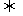 该直角边等于________________
该直角边等于________________
⑶边角关系: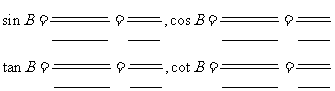
|
|
sinα |
cosα |
tgα |
ctgα |
|
30° |
|
|
|
|
|
45° |
|
|
|
|
|
60° |
|
|
|
|
|
0° |
|
|
|
|
|
90° |
|
|
|
|
|
180° |
|
|
|
|
2、解直角三角形的基本类型:(见下表)
|
类型 |
已知条件 |
解法 |
|
两边 |
两直角边a、b |
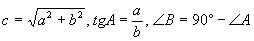 |
|
一直角边a及斜边c |
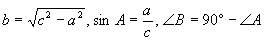 |
|
|
一边一角 |
一直角边a及锐角A |
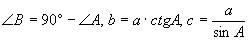 |
|
斜边c及锐角A |
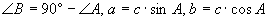 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com