
5.小结
(1)请你说说勾股定理;
(2)勾股定理揭示了“形”与“数”的内在联系。
你还能举例说明这种联系吗?
4.根据教学的具体情况,本节课可以介绍一些古代人民对勾股定理研究以及我国古代数学家对勾股定理的验证做出的伟大贡献的史料.
3.例题教学
课本没有编排例题,教学中可以把本节的练习作为例题.
2.探索活动
(1)猜想图2-1中以AB为边的正方形的面积是多少?说说你是如何猜想的?
通过猜想促使学生积极的思考,主动地进行由邮票图案到图2-1的联想(小方格的数量与正方形的面积、正方形的面积与正方形的边长、正方形的边长与三角形形状的联想),教学中要让学生主动建立由数到形、由形到数的联想,从中使学生不断积累数学活动的经验.
(2)你能说明你的猜想是正确的吗?与同学交流.
(3)从以AB为边的正方形的面积计算中你发现了什么,?
(4)你计算以AB为一边的正方形的面积的方法和小明、小丽的计算方法一样吗?从小明或小丽的计算方法中你得到什么启发?
把图形进行“割”或“补”,两种方法体现的是同一种思想--化归思想,即把不能利用网格线直接计算面积的图形化成可以利用网格线直接计算面积的图形.
(5)从以AB为边的正方形的面积的计算中,我们发现:以AB为边的正方形的面积等于以BC为边的正方形的面积与以:AC为边的正方形的面积的和,在其他的直角三角形中,还有这种关系吗?请你在方格纸上做实验,并与同学交流.
通过学生操作、实验,引导学生将正方形的面积与三角形的边长建立联系.教学中要让学生充分地进行交流.比如,教学中可以请几位同学介绍自己的实验结果,并将数据填入表格(见下表),从而为归纳提供基础,使学生体验归纳的思想.
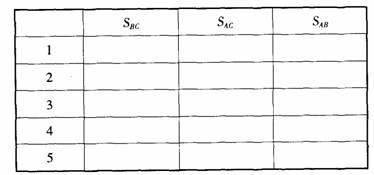
(6)从我们实验的大量数据中,你对直角三角形三边之间的数量关系有什么猜想?
1.情境创设
考虑到邮票源于生活,学生有兴趣;并且纪念毕达哥拉斯学派的纪念邮票非常简明地、必然地将学生的注意引向本节的本质,因此课本用“观察邮票图案小方格的个数,你有哪些发现?”作为本节的情境.教学时,也可以设计其他的情境.
3.经历用多种拼图方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考与表达的能力,感受勾股定理的文化价值.
[教学过程(第一课时)]
2.经历探索勾股定理的过程,发展合情推理的能力,体会数形结合的思想.
1.能说出勾股定理,并能应用勾股定理解决简单问题.
2.1勾股定理
[教学目标]
5、等腰三角形ABC的腰长为10,底边上的高为6,则底边的长为多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com