2.会设计简单的调查问卷收集数据；

1.了解全面调查收集数据的方法；

4.1喜爱哪种动物的同学最多

学习目标点击

知识与技能

3．小结

　　 在“从面积到乘法公式”一章的学习中，我们把几个图形拼成一个新的图形，通过图形面积的计算得到了许多有用的式子．这节课同样地我们用多种方法拼图验证了勾股定理，你有什么感受?

2．探索活动

　　 (1)你能把章头图中的图①、②、③、④、⑤拼成正方形ABDE吗?你能验证勾股定理吗?与同学交流．

　　 (2)剪4个全等的直角三角形，把它们拼成弦图，与同学合作探索数学家赵爽是如何利用弦图验证勾股定理的．

　　 赵爽在《勾股圆方图注》一书中给出的证明：弦图中每一个直角三角形涂朱色，它的面积叫做“朱实”，中间的一个小正方形涂黄色，　 它的面积叫做“中黄实”，也叫“差实”，以弦为边的正方形叫“弦实”．“按弦图，又可以勾股相乘为中黄实，加差实，亦成弦实”，即，

　　 (朱实四)　 (中黄实)(弦实)　　 所以，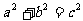

　　 (3)通过拼搭弦图和利用弦图验证勾股定理，你想到了什么?

　　 设计活动(3)促使学生“想”，教学中要引导学生关注弦图与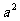、、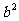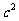的联系，体会弦图是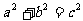的一个图形背景，然后鼓励学生能否给出不同的图形背景．

　　 (4)你能用这4个直角三角形拼搭成不同的图形吗?

　　 (5)利用你拼搭的图形验证勾股定理．

　　 教学中，要让学生进行充分的实践、合作交流．活动(4)是由式到形的过程，活动(5)是从形到式的过程，使学生再一次体验式与形两者间的联系．

1、情境创设

　　 勾股定理是数学中一个重要的定理．几乎所有拥有古代文化的民族和国家都对它进行了大量的研究，找到了许多验证的方法，这些方法不仅验证了勾股定理，而且丰富了人们研究数学问题的方法和策略，促进了数学的发展．

　　 你想了解一些验证勾股定理的方法，并且自己来验证勾股定理吗?让我们一起走进数学实验室！

3．经历用多种拼图方法验证勾股定理的过程，发展用数学的眼光观察现实世界和有条理地思考与表达的能力，感受勾股定理的文化价值．

[教学过程(第二课时)]

2．经历探索勾股定理的过程，发展合情推理的能力，体会数形结合的思想．

1．能说出勾股定理，并能应用勾股定理解决简单问题．

2.1勾股定理

[教学目标]