3.会观察折线图,能应用极差对简单问题做出判断．

2.知道极差的计算方法．

1.了解极差的意义．

试计算下列两组数据的极差：

A组：0, 10, 5, 5, 5, 5, 5, 5, 5, 5；

B组：4, 6, 3, 7, 2, 8, 1, 9, 5, 5．

例1 观察上图，分别说出两段时间内气温的极差．

例2 你的家庭中年纪最大的长辈比年纪最小的孩子大多少岁？

例3　 自动化生产线上，两台数控机床同时生产直径为40.00毫米的零件，为了检验产品质量,从产品中各抽出10件进行测量，结果如下(单位：毫米)．

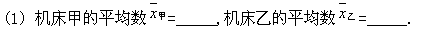
(2) 就所生产的10个零件的直径变化范围,你认为哪个机床生产的质量好?

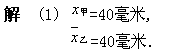
　　 (2) 因为甲的极差为0.12，乙的极差为0.22，所以甲机床生产的质量较好．

下表显示的是某市2001年2月下旬和2002年同期的每日最高气温：

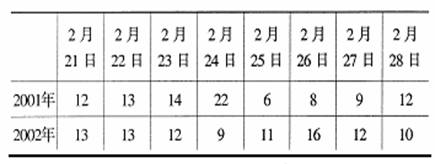
试对这两段时间的气温进行比较．

我们可以由此认为2002年2月下旬的气温比2001年高吗？

两段时间的平均气温分别是多少？平均气温都是12℃．这是不是说，两个时段的气温情况没有什么差异呢？请同学们根据上表提供的数据,绘制出相应的折线图．

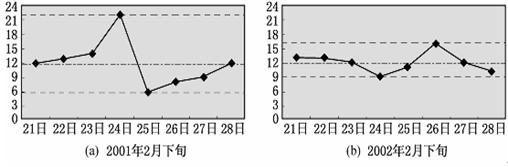
观察一下，它们有差别吗？把你观察得到的结果写在下面的横线上：

_____________________________________________________________．

通过观察，我们可以发现： 图(a)中折线波动的范围比较大--从6℃到22℃，图(b)中折线波动的范围则比较小--从9℃到16℃．

思考

　　 什么样的指标可以反映一组数据变化范围的大小？

　　 我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变围．用这种方法得到的差称为极差(range)．

　　　　　　　　　 　　　　极差＝最大值－最小值．

小明初一时数学成绩不太好，一学年中四次考试成绩分别是75、78、77、76．初一暑假时，小明参加了科技活动小组，在活动中，小明体会到学好数学的重要性，逐渐对数学产生了兴趣，遇到问题时从多方面去思考，深入钻研．因此小明的数学成绩进步很快，初二的一学年中，小明在四次考试的数学成绩是80、85、92、95．

看完这则小通讯，请谈谈你的看法．你以为在这些数据中最能反映学习态度重要性的是哪一对数据?两者相差多少?

引入概念：极差.

4.下面是某工厂工人的生日情况统计方格图，试回答下列问题：

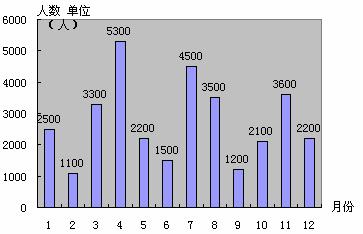
问：生日分布在1-3月份的人数为多少？4-6月份的呢？7-9月份的呢？10-12月份的呢？它们的百分比又分别为几？

3.下面是几次投掷硬币的试验结果，仔细观察并回答下列问题：

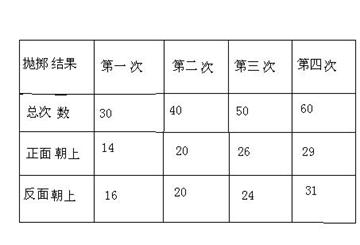
(1)第一次试验中，正面朝上的次数为　　 　，反面朝上的百分比为　　 　。

(2)第二次试验中，反面朝上的次数为　　 　，出现正面的百分比为　　 　。

(3)第三次试验中，正面朝上的百分比为　　 　，反面朝上的百分比为　　 　，两种百分比的和为　　 。

(4)第四次试验中，正面朝上的百分比为　　 　，反面朝上的百分比为　　 ，两种百分比的和为

　　 　。

　(5)四次试验中抛掷硬币的总次数为　　 　，出现反面朝上的总次数为　　 　。

2.在一次优秀干部的评选活动中，得票结果如下表所示。(总票数为50)

候选人	小林	小明	小华	小丽
唱票记录	正正正正一	正		正正正
得票数	21	8	2	19

上表数据显示，小林的得票票数是_____，得票百分比为______;小丽的得票票数是_____,得票百分比为______.