
1.重点:(1)掌握一元二次方程的解法,特别是公式法。(2)培养学生的数学意识及解决简单的实际问题的能力。
2.理解一元二次方程的概念
情感态度与价值观目标:
从生活实际中抽象出数学问题,让学生感受方程是刻画现实世界数量关系的工具,增加对一元二次方程的感性认识.
重点、难点、关键:
1.经历由具体问题抽象出一元二次方程的概念的过程,进一步体会方程是刻画现实世界的一个有效数学模型.
2.一元二次方程的有关概念.
过程与方法目标:
1.一元二次方程的概念
1.花边有多宽(一)
教学目标:
知识与技能目标:
(二)1.预习内容:P47-P48
板书设计:
|
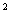 十7
十7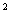 =10
=10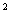 ,
,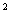 十12x一15=0.
十12x一15=0.|
x |
0 |
0.5 |
1 |
1.5 |
2 |
|
x2+12x―15 |
-15 |
-8.75 |
-2 |
5.25 |
13 |
所以1<x<1.5
进一步计算
|
x |
1.1 |
1.2 |
1.3 |
1.4 |
|
x2+12x―15 |
-0.59 |
0.84 |
2.29 |
3.76 |
所以1.1<x<1.2
因此x 的整数部分是1,十分位是1
(一)课本P46习题2.2 l、2
本节课我们通过解决实际问题,探索了一元二次方程的解或近似解,并了解了近似计算的重要思想--“夹逼”思想.
课本P46随堂练习
1.五个连续整数,前三个数的平方和等于后两个数的平方和,你能求出这五个整数分别是多少吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com