
(x+6)2+72=102,
即x2+12x-15=0.
所以1<x<2.
x的整数部分是1,
|
x |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
2x2-13x+11 |
11 |
4.75 |
0 |
-4 |
-7 |
-9 |
所以x的整数部分是1,十分位是1.
2.一元二次方程的一般形式;ax2+bx+c=0(a≠0)
ax2是二次项,a是系数
bx是一次项,b是系数
c是常数项
三个方程的共同特点:
(1)只含有一个未知数.
(2)整式方程.
(3)可化为ax2+bx+c=0.
3.设梯子底端滑动x m,那么滑动后梯子底端距墙(x+6)m.
根据题意,可得(x+6)2+72=102.
2.设五个连续整数中的第一个数为x,那么后面四个数依次可表示为x+1、x+2、x+3、x+4.
根据题意,可得x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2.
3.关键:根据实际问题确定其值的大致范围.
教学过程:
回顾:1.什么叫一元二次方程?
一元二次方程的一般式是怎样的形式?
问:解花边有多宽的实例以及所提出的问题。
做一做:在前一课的问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72=1。
如图一张长20cm,宽16cm的风景图片,要在它的四周镶上一条同样宽的金色纸边,如果要使金边的面积是图片面积的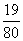 ,金边宽应该是多少?
,金边宽应该是多少?
随堂练习:
随堂练习1.
问:已知直角三角形三边长为三个连续偶数,并且直角三角形面积为24,求这个直角三角形三边长?
课堂小结:
本课时承上一课时的现实问题,探索一元二次方程的过成近似解,发展估算意识和能力,首先解决上一课时提出的第1个问题“花边有多宽”,这个问题解正好是整数。然后解决第3个问题“梯于的底端滑动多少米”,这个问题的解是无理数,应借助解决第1个问题的经验求出近似解,深时作业设计中完成了上一课时的第2个问题.对于几个问题的具体解决,应先根据实际问题确定其解的大致范围。
作业:
课本习题2.2 1.2
2.难点:用估算的方法寻求一元二次方程的解.
1.重点:探究一元二次方程的解或近似解,发展学生估算意识和能力.
3.经历在具体环境中估计一元二次方程解的过程,发展估算意识和能力.
重点、难点、关键:
2.了解一元二次方程及其相关概念,会用配方法、公式法、分解因式法解简单的一元二次方程(数字系数),并在解一元二次方程的过程中体会转化等数学思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com