
2.多项式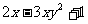 是 ________次________项式,其中最高次项是________,常数项
是 ________次________项式,其中最高次项是________,常数项
是________。
1.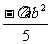 是________次单项式,系数是________。
是________次单项式,系数是________。
7.求代数式的值的步骤
⑴代入,即用数值代替代数式里的字母。
⑵计算,即按照代数式指明的运算顺序,计算出结果。
注意:⑴书写格式,在把字母所取的数值代入代数式时,必须写上“当……时”,表示这个代数式的值是在这种情况下求得的。
⑵求某些代数式的值时,有时采取整体代入法来求。
知识巩固
6.多项式的项及项的系数应包括它前面的符号,比如,多项式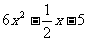 的第二项是
的第二项是 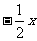 ,而不是
,而不是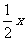 ,第二项的系数是
,第二项的系数是
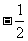 ,而不是
,而不是 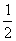 。
。
5.单项式次数仅与单项式中所有字母的指数有关,而与系数无关。单项式中单独出现的字母,其指数“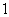 ”通常略去不写,但计算次数时不可丢失。如
”通常略去不写,但计算次数时不可丢失。如
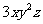 的次数是
的次数是 次,而不是
次,而不是 次。
次。
4.单项式是由数字因数和字母因式两部分组成。数字因数就是单项式的系数。单项式的系数应包括前面的符号,比如单项式
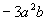 的系数是“
的系数是“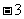 ”而不是“
”而不是“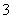 ”。单项式的系数是“
”。单项式的系数是“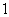 ”或“
”或“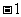 ”时,“
”时,“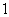 ”通常省略不写,“
”通常省略不写,“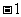 ”中的“
”中的“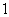 ”也通常省略不写,但“-”号不能省略。因此只含有字母因式的单项式不能认为它们没有系数,它们的系数是“
”也通常省略不写,但“-”号不能省略。因此只含有字母因式的单项式不能认为它们没有系数,它们的系数是“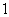 ”或“
”或“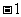 ”。
”。
3.单项式和多项式的判定方法
不含加号或减号的整式就是单项式,含加号或减号的整式就是多项式。
2.整式的判定方法
分母不是字母的代数式就是整式。分母是字母的代数式就不是整式。如 ,
,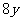 ,
,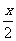 ,
,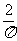 都是整式,
都是整式,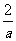 ,
,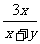 都不是整式。
都不是整式。
1.代数式的判定方法
不含等号,也不含不等号的式子就是代数式。含等号,或含不等号的式子就不是代数式。如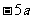 ,
,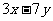 都是代数式;
都是代数式;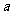 >2,
>2,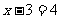 都不是代数式。
都不是代数式。
4.单项式与多项式统称为整式。即单项式、多项式都是整式。
重点剖析
例1 下列代数式: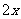 ,
, ,
,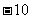 ,
,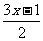 ,
,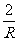 ,
,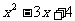 ,
,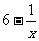 ,
,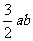 ,其中哪些是单项式?哪些是多项式?哪些是整式?
,其中哪些是单项式?哪些是多项式?哪些是整式?
解: 单项式: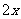 ,
,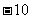 ,
, 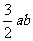 ;
;
多项式: ,
,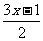 ,
,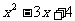 ;
;
整式: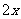 ,
, ,
,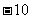 ,
,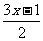 ,
,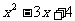 ,
,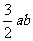 。
。
注意:⑴整式是单项式与多项式的统称。⑵分母中含有字母的代数式一定不是整式,也就一定不是单项式,也不是多项式。
例2 说出下列多项式的项,并说明是几次几项式:
⑴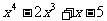 ;⑵
;⑵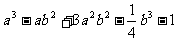 。
。
解:⑴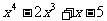 的项是
的项是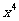 、
、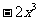 、
、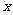 、
、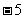 ,它是四次四项式。
,它是四次四项式。
⑵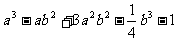 的项是
的项是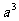 、
、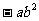 、
、 、
、 、
、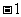 ,它是四次五项式。
,它是四次五项式。
注意:⑴多项式的项包括前面的符号;⑵在求多项式的次数之前要先确定每一项的次数,其中次数最高项的次数就是这个多项式的次数;⑶常数项的次数为 。
。
例3 已知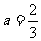 ,
,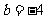 ,求代数式
,求代数式 的值。
的值。
解:当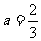 ,
,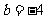 时,
时,

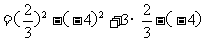
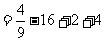
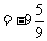 。
。
注意:⑴将相应的字母换成数字,运算符号、原来的数字不变。⑵如果字母给出的数值是负数,代入时必须加括号。⑶如果字母给出的数值是分数,作乘方运算时也必须添上括号。⑷如果代数式中省略了乘号,代入数值后必须添上乘号。
例4 已知代数式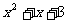 的值为
的值为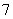 ,求代数式
,求代数式 的值。
的值。
分析:若由条件先求出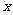 值,再代入
值,再代入 中计算,则很麻烦,并且到现在为止我们还不会解
中计算,则很麻烦,并且到现在为止我们还不会解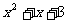
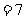 这个方程。可由条件求得
这个方程。可由条件求得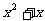
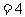 ,再将要求值的代数式进行变形,然后整体代入求值。
,再将要求值的代数式进行变形,然后整体代入求值。
解:∵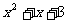
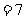 ,∴
,∴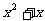
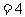 ,
,
∴ =
=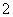 (
(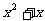 )
)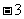 =
=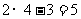 。
。
注意:本题通过将代数式变形,然后“整体代入”来求代数式的值。“整体代入”不是求出代数式里各个字母的值,而是把与这些字母有关的某个代数式的值整体代入,达到求解的目的。
错点反思
例5 指出下列单项式的系数和次数:⑴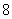 ;⑵
;⑵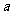 ;⑶
;⑶ 。
。
错解:⑴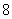 的系数是
的系数是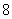 ,次数是
,次数是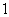 ;
;
⑵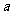 的系数和次数都是
的系数和次数都是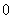 ;
;
⑶ 的系数是
的系数是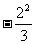 ,次数是6。
,次数是6。
反思:⑴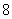 的系数是
的系数是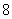 ,其中不含字母所以次数不是1,而是0;⑵单独一个字母
,其中不含字母所以次数不是1,而是0;⑵单独一个字母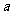 的系数和次数都是1,次数不是0;⑶误认为
的系数和次数都是1,次数不是0;⑶误认为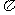 是字母,实际上
是字母,实际上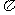 是常数,不是字母,所以
是常数,不是字母,所以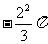 是系数,次数为5。
是系数,次数为5。
正解:⑴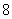 的系数是
的系数是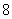 ,次数是0;
,次数是0;
⑵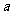 的系数和次数都是
的系数和次数都是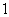 ;
;
⑶ 的系数是
的系数是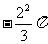 ,次数是
,次数是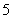 。
。
注意:⑴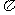 是常数,不是字母;⑵单项式的次数是所有字母的指数和,不能加上系数中的指数;⑶若单项式是单独的一个数字,则它的系数是它本身,次数是0。
是常数,不是字母;⑵单项式的次数是所有字母的指数和,不能加上系数中的指数;⑶若单项式是单独的一个数字,则它的系数是它本身,次数是0。
例6 用代数式表示:
⑴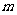 与
与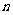 的4倍的和;⑵
的4倍的和;⑵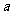 与
与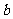 平方差;⑶比
平方差;⑶比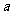 大20%的数。
大20%的数。
错解:⑴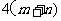 ;⑵
;⑵ ;⑶
;⑶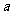 +20%。
+20%。
反思:⑴混同了“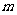 与
与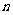 的和的4倍”;⑵混同了“
的和的4倍”;⑵混同了“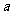 与
与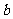 的平方的差”;⑶错在将百分数等同于一般的数。
的平方的差”;⑶错在将百分数等同于一般的数。
正解:⑴ ;⑵
;⑵ ;⑶(1+20%)
;⑶(1+20%)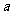 。
。
注意:列代数式时要弄清楚题中的数量关系,运算顺序,书写代数式时要规范。
方法总结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com