
2.单项式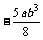 的系数是
,次数是
;当
的系数是
,次数是
;当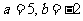 时,这个代数式的值是________.
时,这个代数式的值是________.
1.“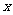 的平方与2的差”用代数式表示为_____
___.
的平方与2的差”用代数式表示为_____
___.
课本76―77:3⑵⑷⑹,4⑵⑷⑹⑻,6,8,9
板书设计:
|
教学后记:
①本节是全章的复习课.首先是复习本章的主要概念和法则.在上节课所留复习作业的基础上,一上课,就进行课堂提问,“关于单项式,你都知道什么”,“关于多项式,你又知道什么”.通过学生的回答,既可检查学生作业完成的情况,又充分地调动学生积极性,使学生主动参与到课堂中来.而且这样的问题具有一定的开放性,可使学生的思维发散,把他们所知道的有关内容都说出来.通过对一个问题的多个侧面地回答,可进一步加深学生对基础知识的理解与重视,又可培养他们主动分析问题的习惯.
②对于应该强调的问题,如果只是泛泛而谈,效果不大.因此,在复习了本章的主要知识后,出了一组练习,通过具体的题目,强调有关的问题,将给学生留下更深的印象,学习效果会更好.
3.课堂练习:
课本p76―77:1,2, 3⑴⑶⑸,4⑴⑶⑸⑺,5,7
1.例题:
例1:找出下列代数式中的单项式、多项式和整式.
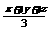 ,4xy,
,4xy,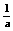 ,
,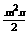 ,x2+x+
,x2+x+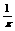 ,0,
,0,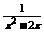 ,m,―2.01×105
,m,―2.01×105
解:单项式有4xy,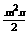 ,0,m,―2.01×105;多项式有
,0,m,―2.01×105;多项式有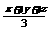 ;
;
整式有4xy,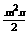 ,0,m,-2.01×105,
,0,m,-2.01×105,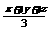 .
.
此题由学生口答,并说明理由.通过此题,进一步加深学生对于单项式、多项式、整式的定义的理解.
例2:指出下列单项式的系数、次数:ab,―x2, xy5,
xy5,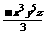 .
.
解:ab:系数是1,次数是2; ―x2:系数是―1,次数是2;
 xy5:系数是
xy5:系数是 ,次数是6;
,次数是6; 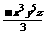 :系数是―
:系数是―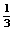 ,次数是9.
,次数是9.
此题在学生回答过程中,及时强调“系数”及“次数”定义中应注意的问题:系数应包括前面的“+”号或“―”号,次数是“指数之和”.
例3:指出多项式a3―a2b―ab2+b3―1是几次几项式,最高次项、常数项各是什么?
解:是三次五项式,最高次项有:a3、―a2b、―ab2、b3,常数项是―1.
例4:化简,并将结果按x的降幂排列:
(1)(2x4―5x2―4x+1)―(3x3―5x2―3x); (2)―[―(―x+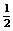 )]―(x―1);
)]―(x―1);
(3)―3(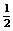 x2―2xy+y2)+
x2―2xy+y2)+ 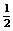 (2x2―xy―2y2).
(2x2―xy―2y2).
解:(1)原式=2x4―3x2―x+1; (2)原式=―2x+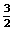 ; (3)原式=―
; (3)原式=―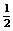 x2+
x2+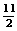 xy―4y2.
xy―4y2.
通过此题强调:(1)去括号(包括去多重括号)的问题;(2)数字与多项式相乘时分配律的使用问题.
例5:化简、求值:5ab―2[3ab―(4ab2+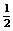 ab)]―5ab2,其中a=
ab)]―5ab2,其中a=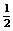 ,b=―
,b=―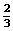 .
.
解:化简的结果是:3ab2,求值的结果是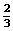 .
.
例6:一个多项式加上―2x3+4x2y+5y3后,得x3―x2y+3y3,求这个多项式,并求当x=―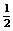 ,y=
,y=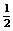 时,这个多项式的值.
时,这个多项式的值.
解:此多项式为3x3―5x2y―2y3;值为―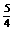 .
.
2.主要法则:
①提问:在本章中,我们学习了哪几个重要的法则?分别如何叙述?
②在学生回答的基础上,进行归纳总结:
整式的加减
1.主要概念:
(1)关于单项式,你都知道什么?
(2)关于多项式,你又知道什么?
引导学生积极回答所提问题,通过几名同学的回答,复习单项式的定义、单项式的系数、次数的定义,多项式的定义以及多项式的项、同类项、次数、升降幂排列等定义.
 (3)什么叫整式?
(3)什么叫整式?
在学生回答的基础上,进行归纳、总结,用投影演示:
整式

板书设计:
|
教学后记:
通过实际问题,让学生经历一个实际背景,去体会进行整式的加减的必要性。通过“去括号、合并同类项”习题的复习归纳总结出整式的加减的一般步骤,培养学生的观察、分析、归纳和概括的能力,掌握知识的发生发展过程,理解整式的加减实质就是去括号、合并同类项。教学过程中由学生小组讨论概括出整式的加减的一般步骤,然后出示例题,由学生解答,同时采取由学生出题,其他同学抢答等形式,来提高学生的学习兴趣,充分发挥他们的主观能动性,提高课堂教学效益。
4.数学是解决实际问题的重要工具。
3.求多项式的值,一般先将多项式化简再代入求值,这样使计算简便。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com